FABRICACIÓN DE ESTRUCTURAS DE UNIÓN P-N LOCAL EN MONO CRISTALES DE CuInSe2 MEDIANTE LA APLICACIÓN DE ALTOS CAMPOS ELÉCTRICOS
Saludos mis estimados amigos de la comunidad de steemit acá les presento el planteamiento del trabajo que lleva por nombre :
FABRICACIÓN DE ESTRUCTURAS DE UNIÓN P-N LOCAL EN MONO CRISTALES DE CuInSe2 MEDIANTE LA APLICACIÓN DE ALTOS CAMPOS ELÉCTRICOS.
Presentado por:
Alfonso R Romero R
Maracaibo
ÍNDICE
INTRODUCCION
- MARCO TEORICO
- HIPOTESIS
- OBJETIVOS17
- METODOLOGIA
- VIABILIDAD
BIBLIOGRAFIA
INTRODUCCIÓN
El interés en el estudio de los materiales semiconductores, tanto en su fabricación como en sus propiedades, está perfectamente justificado por las aplicaciones tecnológicas basadas en estos materiales. Los semiconductores I-III-VI2 son conocidos por su potencial para ser aplicados como células fotovoltaicas, diodos emisores de luz (LEDs), y dispositivos de óptica no lineal.
El silicio y el germanio, pertenecientes al grupo IV de la tabla periódica, surgen como los semiconductores básicos, teniendo como extensión natural, según la regla de Grimm-Sommerfeld o de cuatro electrones promedio por átomo:

Donde:

A los semiconductores binarios, sean los de la familia:

O los de la familia:

A su vez, los semiconductores ternarios de la familia I-III-VI2 son la extensión lógica de la familia II-VI, cristalizando en la estructura tetragonal de la calcopirita que se deriva directamente de la zincblenda.
En particular, el CuInSe2 que es un miembro de la familia I-III-VI2, es un compuesto ideal para la fabricación de células solares excepto por el hecho de que su brecha prohibida es pequeña. Esta limitación puede resolverse realizando aleaciones con materiales semiconductores de la misma familia pero con brechas mayores de energía, como el CuGaSe2 de tal manera que se aumente la brecha del CuInSe2 pero conservando las excelentes propiedades de dicho material para células fotovoltáicos. (1-3)
Aunque se han realizado numerosos estudios sobre los procesos de fabricación, propiedades eléctricas y ópticas de los dispositivos fotovoltáicos utilizando como material base al CuInSe2, en la literatura existen muy pocos reportes sobre los mecanismos de conducción que dominan estas propiedades en tales dispositivos. En general, se conoce muy poco sobre el origen de las propiedades de transporte de estos materiales, lo cual no ha permitido el desarrollo de tecnología adecuada que permita reducir costos, y hacer el material económicamente competitivo.
El primer paso para el estudio de las propiedades de cualquier nuevo dispositivo, empieza por la determinación de los parámetros físicos que dominan las propiedades de transporte de dicho semiconductor. En otras palabras, es imprescindible la fabricación de contactos metal-semiconductor que conlleven a la producción de contactos óhmicos y/o rectificadores confiables; ya que estas estructuras son inevitables y se presentan en cualquier tipo de dispositivos a fabricar. Además, las estructuras tipo Schottky, como se le denomina al contacto metal-semiconductor, se utiliza como herramienta de investigación en la determinación de parámetros físicos.
En este trabajo se llevará a cabo el estudio de los mecanismos de conducción que dominan las propiedades eléctricas en algunas estructuras metal-semiconductor fabricado en el semiconductor CuInSe2.
MARCO TEÓRICO.
Teoría Básica de las Uniones p-n.
Las uniones p-n son de gran importancia en las aplicaciones de la electrónica moderna y en el entendimiento de otros dispositivos. Dicha teoría establecida por Schokley y Moll en 1958, sirve como fundamento básico para la física de dispositivos semiconductores.
La unión p-n puede ser vista como dos materiales, tipo n y p, que han sido traídos a contacto íntimo. Como los electrones son abundantes en el material tipo n, estos se difunden hacia el material tipo p:
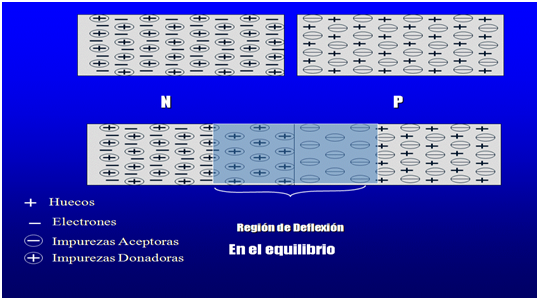
El mismo proceso ocurre a los huecos del material tipo p. Este flujo de cargas establece un campo eléctrico que comienza a aminorar el proceso de difusión hasta que se establece el equilibrio. El diagrama de la banda de energía para el caso en equilibrio se muestra en la figura 1b.
Ya que el número de cargas totales en el proceso deben conservarse, se tiene que para la unión abrupta se debe cumplir:
WdpNA=WdnND (1)
Tal como se muestra en la figura 1c.
Donde:
Wdp: es el ancho de la región de deflexión en el lado P.
Wdn: es el ancho de la región de deflexión en el lado N.
NA: densidad de concentración de impurezas aceptoras.
ND: densidad de concentración de impurezas donadoras.
Un parámetro importante es el potencial interno bi que se crea al formarse la unión. De acuerdo con la figura 1b, este parámetro surge de la suma de Bn y Bp, lo cual da como resultado:
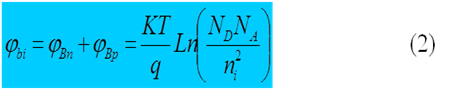
Este parámetro presenta por definición la deformación de la banda de energía en equilibrio.
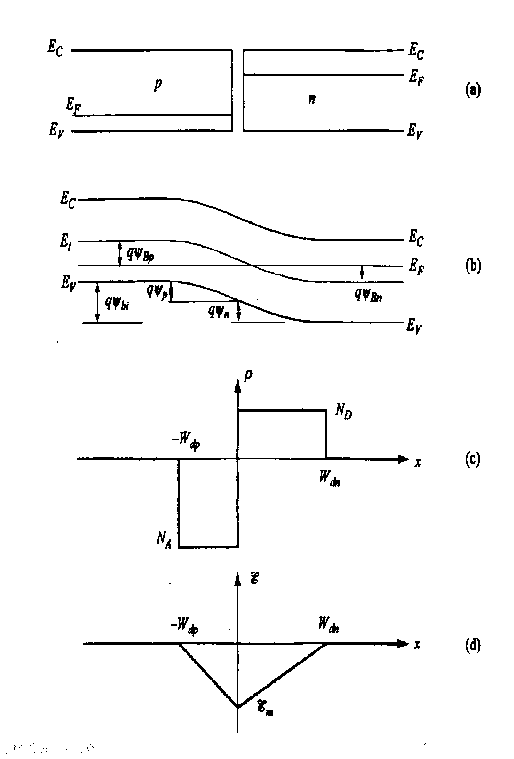
FIGURA No.1: Formación de una unión p-n al traer dos materiales aislados n y p (a) a contacto íntimo (b). La variación de potencial (c) es el resultado de la redistribución de cargas, o redistribución de campo eléctrico (d) en la región de deflexión.
Utilizando la ecuación de Poisson y las condiciones de frontera adecuadas, es posible obtener el siguiente conjunto de ecuaciones para una unión p-n bajo un voltaje aplicado:
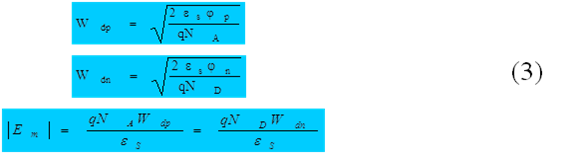
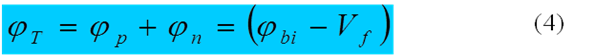
La ecuación 4 puede ser interpretada como el área debajo de la curva de campo – distancia en la figura 1d.
En dispositivos prácticos usualmente un lado de la unión tiene una concentración de `portadores mayores que el otro, y la unión puede ser tratada como una unión de un solo lado. En este caso el ancho de la deflexión y la variación de potencial en el lado de mayor concentración puede despreciarse.
La figura 2, donde se muestra el diagrama de bandas y la concentración de portadores cuando se aplica voltaje, se utiliza para derivar la característica corriente-voltaje de la unión p-n. La corriente en polarización directa de una unión p-n está determinada por la difusión de portadores minoritarios inyectados. La concentración en el borde de la región de deflexión viene dada por:
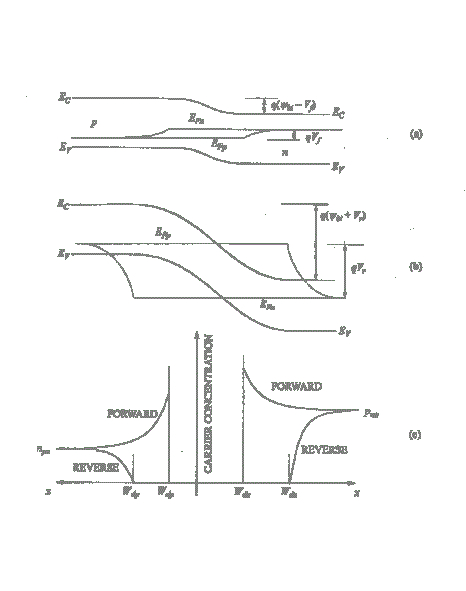
FIGURA No. 2 :banda de energía de una unión p-n, (a) en polarización directa y (b) en polarización inversa, (c) perfil de concentración de portadores minoritarios en polarización directa e inversa.

Combinando la ecuación de continuidad con la ecuación de corriente, asumiendo estado estacionario, rata de generación cero y corriente de drenaje cero, se obtiene:

Donde X=0 corresponde al borde de la región de deflexión. Resolviendo las ecuaciones diferenciales se obtiene el perfil de portadores minoritarios:
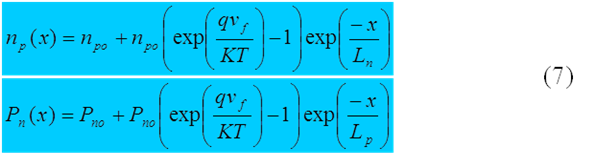
Las dos corrientes de difusión dan una corriente total de:
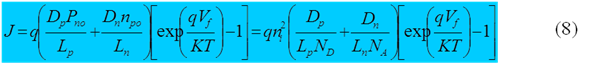
A cada lado de la unión la corriente de difusión es una función de la distancia.
Esta se ve maximizada en x=o, de donde se obtiene la ecuación 8. Ya que la corriente tiene que ser continua, la corriente de difusión se ve suplementada por una corriente de drenaje de los portadores mayoritarios. Esta ecuación es válida además para el caso de la polarización inversa cuando Vf es negativo. En los casos en que los espesores de las regiones n o p son menores que la longitud de difusión de los portadores Lp o Ln, estos parámetros deben ser remplazados por los espesores correspondientes en la ecuación 8 lo cual produce un incremento de la corriente.
Las características I-V descrita por la ecuación 8 se muestra en la figura 3. En polarización directa, la corriente aumenta de manera exponencial con Vf hasta que la pendiente se hace más gradual. Esto puede ser debido a inyección de portadores a altos niveles tal que el voltaje aplicado no se desarrolla totalmente en la región de deflexión. La resistencia en serie Rs puede causar el mismo efecto. En la polarización inversa, puede ocurrir el perforamiento de la barrera por ionización por impacto o por tunelaje del tipo Zener. Estos mecanismos pueden ser identificados por su dependencia con la temperatura. A alta temperatura la rata de ionización disminuye y el voltaje de perforación debido a la avalancha por multiplicación se incrementa. La dependencia opuesta se observa en el caso de perforamiento del tipo Zener. Normalmente la multiplicación por avalancha ocurre primero.
Un componente adicional de la corriente de la ecuación 8 es debida al proceso de recombinación/generación a través de estados intermedios dentro de las bandas prohibidas, dentro de la región de deflexión. Este mecanismo da origen a una corriente descrita por la siguiente ecuación:

Si el término qniWd/2t es comparable o más grande que el factor pre - exponencial en la ecuación 8, la corriente para pequeños valores de Vf en ambas polarizaciones se verá incrementada.
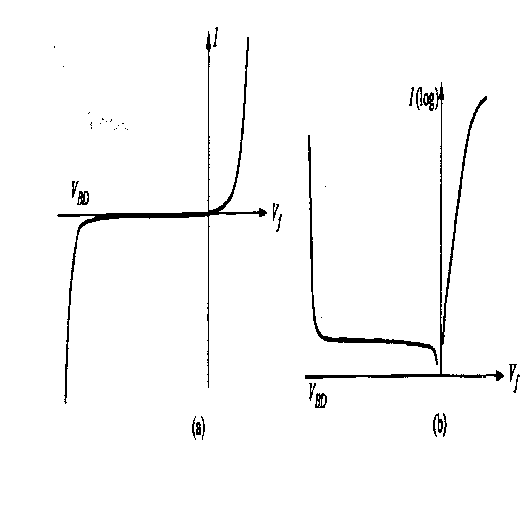
FIGURA No.3: Característica I-V de una unión p-n en escala lineal (b) y en escala logarítmica (b).
ESTRUCTURAS METAL –SEMICONDUCTOR (MS)
El contacto MS es la estructura más importante dentro de los dispositivos electrónicos, esto es debido a que todo dispositivo semiconductor debe conectarse al mundo exterior a través de un contacto metálico.
Cuando se realiza dicho contacto pueden surgir dos tipos de comportamiento en las características corriente-voltaje del dispositivo. El primero puede ser un comportamiento lineal, denominado contacto óhmico, donde se produce por lo general variaciones relativamente grandes de la corriente con variaciones pequeñas del voltaje. El segundo comportamiento es del tipo no lineal, dando origen a una serie de estructuras con aplicaciones específicas.
La unión metal-semiconductor (MS) es más comúnmente conocida como diodo de barrera Schottky, algunas veces es llamado también diodo de barrera de superficie o diodo de portadores o electrones calientes.
Las primeras versiones del diodo Schottky fueron fabricadas en forma de contacto puntual con un alambre de metal, llamado bigote o pelo de gato, el cual se coloca a presión sobre la superficie del semiconductor como se muestra en la siguiente figura

Dependiendo del proceso de fabricación del contacto puntual, la característica del dispositivo puede ser el de una unión p-n o el de un diodo de barrera Schottky. Esta estructura resultó ser inestable y poco reproducible, así que fue reemplazada poco a poco por la deposición al vacío de metales.

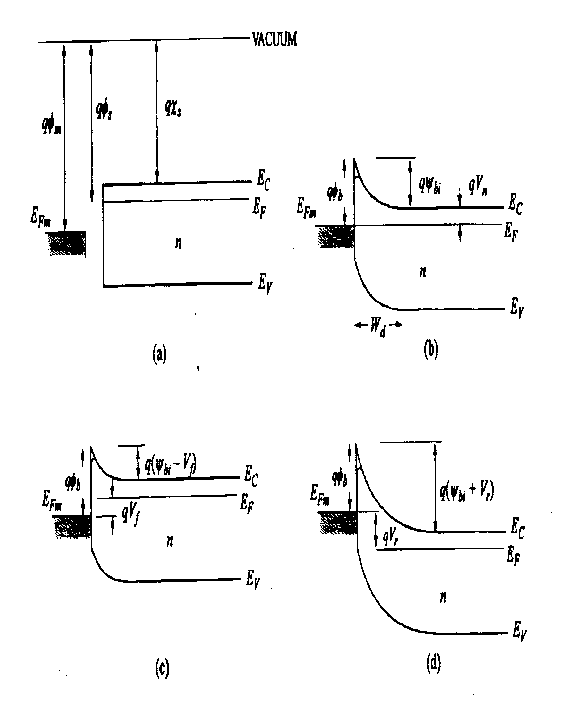
FIGURA No.4: Banda de energía de una estructura metal-semiconductor. (a) metal y semiconductor aislado, (b) materiales conectados y bajo equilibrio. (c) polarización directa de la estructura y, (d) polarización inversa.
La formación de un diodo de barrera Schottky se muestra en el diagrama de energía de la figura 4. Asumiéndose una interfase ideal, la altura de la barrera debería estar dada por:
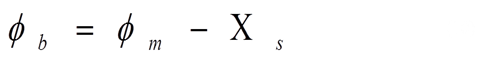
Donde m representa la función trabajo de metal y Xs la función de trabajo del semiconductor. Sin embargo, desde el punto de vista experimental en muy raras ocasiones dicha relación se cumple exactamente.
La discrepancia todavía no está totalmente entendida. En la actualidad existen algunas propuestas para explicar esta discrepancia donde se consideran (i) una capa aislante en la interfase, (ii) trampas superficiales, (iii) estados inducidos en la brecha prohibida por el metal y por último (iv) dipolos en la interfase dependiente de la estructura. Como resultado de todo esto, la formación de una barrera tiene muy poca dependencia de la función trabajo del metal que se utilice.
El transporte de corriente de un contacto MS es debido principalmente a los portadores mayoritarios, a diferencia de las uniones p-n donde son los portadores minoritarios lo que gobiernan el transporte de cargas.
En el contacto MS se producen cuatro procesos básicos de transporte que son:
• Transporte de electrones desde el semiconductor sobre la barrera de potencial hacia el metal, este el comportamiento típico del diodo Schottky en semiconductores moderadamente dopados.
• Tunelaje mecánico cuántico a través de la barrera de potencial que es típico de semiconductores altamente dopados.
• Recombinación en la región del espacio de carga, que es el mismo proceso que presentan las uniones p-n.
• La inyección de huecos desde el metal hacia el semiconductor que es equivalente a la recombinación en la región neutral de una unión p-n.
Debido a su importancia para las aplicaciones en corrientes directas, microondas y como herramientas en el análisis de otros parámetros físicos fundamentales, los contactos metal-semiconductor se han estudiado extensivamente y representan en todo caso, la primera herramienta seria en el estudio de nuevos dispositivos y materiales semiconductores. Además de las inmensas aplicaciones de los dispositivos Schottky, los contactos MS han sido utilizados específicamente como electrodos de transistores de efectos de campo (MESFET), como contacto de fuente y drenaje en MOSFET, como electrodos de osciladores de alta potencia IMPATT, como tercer terminal en dispositivo de transferencia de electrones, y como fotodetectores y células solares.
CAPACITANCIA DE BARRERA (CT) EQUIVALENTE PARA LA UNION PN
Si el diodo se considera como un dispositivo en el cual no hay almacenamiento de cargas su comportamiento puede asemejarse al de un dispositivo infinitamente rápido. En este caso, al aplicar un escalón de corriente el dispositivo no tendrá inercia de carga, y la corriente podrá cambiar en forma instantánea y en tiempo cero. Este comportamiento no sucede en la práctica porque existen efectos de almacenamiento de cargas en el dispositivo. Básicamente, hay dos formas de almacenamiento de cargas:
• carga almacenada en la región de agotamiento debida a la concentración de dopantes,
• carga almacenada debida a la concentración de portadores minoritarios inyectados en las regiones neutras.
Estas cargas pueden asociarse a dos capacitancias por unidad de área llamadas: capacidad de juntura o de barrera (CT) y capacidad de difusión (Cd), respectivamente.
Capacidad de barrera CT
La capacidad CT proviene de la región de agotamiento donde se forma una capa dipolar de carga fija positiva y negativa debida a los átomos donadores y aceptores ionizados. Recordemos que una polarización inversa (VR) produce un incremento en el ancho de la región de carga espacial (w), y por lo tanto un incremento de carga por unidad de área:
dQ = q xn ND = q xp NA
donde:

La expresión anterior también puede escribirse en la forma:

que es la expresión de la capacitancia por unidad de área de un capacitor de placas planas paralelas de separación w con un dieléctrico de permitividad .
HIPÓTESIS.
• Es posible Fabricar estructuras de unión p-n local en monocristales de CuInSe2 mediante la aplicación de altos campos eléctricos.
• Es posible determinar a partir del análisis de la característica corriente-voltaje el tipo de mecanismo que dominan las propiedades eléctricas del material.
• Es posible determinar a partir de la característica corriente-voltaje y la capacitancia-voltaje la altura de la barrera que determina las propiedades de los contactos óhmicos y rectificadores.
OBJETIVOS.
General:
Fabricar estructuras de unión p-n local en monocristales de CuInSe2 mediante la aplicación de altos campos eléctricos.
Específicos:
• Determinar la característica corriente-voltaje en las estructuras p-n de CuInSe2.
• Determinar la característica capacitancia-voltaje en las estructuras p-n de CuInSe2.
METODOLOGÍA
- Se procederá a la síntesis del CuInSe2 por fusión directa de los elementos químicos constituyente en cantidades estequiométricas.
- Se preparan estructuras metal-semiconductor por electrodeposición de Oro, Cobre, Níquel y por aleación térmica de cadmio, indio y estaño.
- Utilizando una fuente de voltaje programable y un pico amperímetro se medirá la característica corriente-voltaje de las estructuras metal-semiconductor.
- Utilizando un analizador de capacitancia-voltaje se determinará dicha característica en cada una de las estructuras metal-semiconductor que presentan fenómeno de rectificación.
- Se analizarán los resultados y se establecerán los mecanismos de conducción dominantes en el material.
- Se establecerán conclusiones y se redactará el trabajo especial de grado.
FUNDAMENTO Y VIABILIDAD
El Laboratorio de Ciencia de los Materiales dispone de la infraestructura de investigación necesaria para llevar a cabo todos los experimentos propuestos. Además el tutor y cotutor poseen amplia experiencia en esta área como de los recursos bibliográficos y metodológicos a ser empleados.
REFERENCIAS BIBLIOGRÁFICAS
- PABLO E. NARANJO MUÑOZ Y JAIRO ARBEY RODRIGUEZ MARTINEZ, Propiedades Ópticas de CuInSe2 y CuGaSe2 usando DTF, REVISTA COLOMBIANA DE FÍSICA, VOL. 38, No. 3. 2006
- KWOJK K. NG. Complete Guide to Semiconductors Devices, McGraw Hill, New York (USA) .Pp 564-565.1995.
- J.L.SHAY AND J.H. WERNICK, Ternary Chalcopyrite Semiconductors: Growth, Electronic Properties and Applications, 5th edition, Pergamon Press, 1975, pp:3.
- LEU I. BERGER AND VITALII D. P.., Ternary Diamond – Like Semiconductors, Consultants Bureau, , New York (London), 1969.
- D. A. Neamen, Semiconductor Physics and Devices, Basic Principles, McGraw Hill, University of New Mexico, pp 238-261. 2003
- S. Mehdaoui a,*, O. Aissaoui et al., Contribution study of properties of copper indium diselenide thin .lms, Vacuum 82 (2008) 1194–1197
- WASIM S. M., Solar Cells 16: 289-316, 1986.
- ROCKETT A., BIRKMIRE R. W. J. Appl Phys 70: R81-R97, 1991.
- DURANTE RINCÓN C. WASIM S. M., FONTAL B. Y HERNÁNDEZ E. Ciencias 5(1): 45-49, 1997.
- DURANTE RINCÓN C. WASIM S. M., HERNÁNDEZ E. Cryst Res Tecnol, 31: S241-245. 1996
- HEDSTRÖM J., OHLSÉN H., BODEGÂRD M., KYLNER A., STOLT L., HARISKOS D., RUCKH M. AND SCHOCK H. W. 23rd IEEE Photovoltaic Special Conf., 1993.
- CAHEN D., GILET J. M., SCHMITZ C., CHERNYAK L., GARTSMAN K. AND JAKUBOWICZ A. Science 258, 271., 1992.
- CHERNYAK L., CAHEN D., ZHAO S., HANEMAN D. Appl. Phys. Lett. 65 (4) 1994.
- HERNÁNDEZ E. Cryst. Res. Technol. 33 (2), 285-289. 1998.
- LAMPERT M. A. AND MARK P., Current Injection in Solids (Academic New York) 1970.
- ROBERTS G. I. AND C.R. CROWELL. J. Appl. Phys. 41, 1767, 1970.
- SCHAUER F., NESPUREK S. AND VALERIÁN K. J. Appl. Phys. 80, (2), 880, 1996.
- SHOCKLEY W., Bell Syst. Techn. J. 28, 435, 1949.
- SZE S. M. Physics of Semiconductor Devices, 2nd Edition, John Wiley & Sons (1981) PP 74-96.
- ZMESKAL O., SCHAUER F., NESPUREK D. J., J. Phys. C : Solid State Phys. 18, 1873, 1985.
- ROBERTS G. I. AND C.R. CROWELL. Solid State Electron., 16, 29, 1973.
Bueno mis amigos Steemians, no olvides dejar tu comentario, en un próximo post les presentare la culminación de esté, los resultados y conclusiones...
Espero haya sido de su agrado @iamphysical , nos vemos en un próximo post.
Nos seguimos leyendo en un próximo post.
Interesante su post recuerda pasar por mi perfil espero tu sea de Tu beneficio…!!! Upvoted
Ok gracias lo haré...
El estudio de los semiconductores es una línea de investigación muy amplia e importante en la Física del Estado Sólido, así que tus conocimientos pueden ser de interés para la comunidad científica #stem-espanol. Te recomiendo transcribir el texto de tus láminas PowerPoint para verificar si hay contenido similar en la WEB y poder evaluar tu contribución. Saludos mi estimado @alfrichreyes
Ok yovani @iamphysical, lo haré apenas pueda, Gracias...