📢 Sonido [Vibración]: Explicación desde la Fisica ✔ | Primera Parte |
Queridos Steemians !!, es hora de una ciencia divertida otra vez. He estado pensando acerca de lo que será esta publicación durante los últimos dos días. La primera idea fue escribir sobre sonido y luego me di cuenta de que ese tema es realmente enorme y que una publicación sería demasiado larga. Me di cuenta de que antes del sonido debería explicar las ondas primero y en mi próxima lección pasar al sonido. Eso estuvo bien, pero no hay comprensión de las ondas sin vibración y movimiento periódico primero. Entonces, elegí la vibración. Antes de comenzar, aquí hay una lista de publicaciones publicadas anteriormente en mi blog Tópicos de Ciencia:
Scientific Method: Theory or practice
Los genetistas Crean una Tecnología de Edición de Genes Tipo Parque jurásico
Desafios De Ingenieria Para Autos Del Futuro
Science and Health | Sudden death syndrome in Babys
Para seguir este post, no es necesario ningún conocimiento previo de física, sin embargo, este post será necesario para comprender aquellos que lo seguirán, así que piense en esto como lección 1, ondas como lección 2 y finalmente, sonido como la lección 3. Disfruta la publicación y no dudes en contactarme si tienes alguna pregunta o quieres saber más. ¿Estás listo para aprender sobre la vibración? ¡Vamonos!


Cuando las cosas vibran, se mueven hacia adelante y hacia atrás desde su posición de equilibrio. Esa es la misma posición en la que estaría un objeto si no se moviera en absoluto, la posición donde la fuerza neta en ese objeto es cero. Entonces, si tenemos un objeto que puede vibrar y aplicamos una fuerza externa sobre él para perturbar ese estado de equilibrio, comenzará a alejarse del equilibrio, se detendrá en algún punto y volverá al equilibrio, lo pasará y se moverá al del otro lado, luego para y vuelve, y así sucesivamente...

Vemos vibración en todas partes, en nuestras vidas a diario. Desde muñecos cabeza loca en nuestros autos, relojes de péndulo, bolas rebotando en paredes o pisos, niños en columpios, árboles balanceándose con el viento o cualquier otro movimiento de sacudidas y balanceo. Generalmente se trata de una cosa elástica o una que cuelga de algo así como un péndulo. Todos estos son ejemplos que podemos ver, pero si profundizamos encontraremos que, de hecho, todo vibra, incluso objetos sólidos que parecen estar quietos. En sólidos, las partículas también vibran y solo a la temperatura de cero absoluto (-273 ° C) se detienen todos los movimientos. Debido a que he cubierto electrones en mis publicaciones anteriores, esta vez me limitaré a la macrofísica y analizaré la vibración y el movimiento periódico que podemos ver claramente.

Cuando las vibraciones son regulares y repetidas, las categorizamos como periódicas. Un objeto se mueve sobre la misma trayectoria en el transcurso del tiempo y el movimiento se repite hasta que la amortiguación lo detiene. La masa en un resorte y los péndulos son los mejores ejemplos para aprender sobre el movimiento periódico, así que veamos la masa en un resorte. Está en el gif directamente desde este texto.
Mire esa animación y elija una posición inicial en la que se encuentra la masa. Para estar en la misma página con esto, comencemos con la masa en la parte inferior. A partir de ahí, irá al equilibrio, lo pasará y continuará subiendo donde se detendrá y cambiará de dirección y comenzará a regresar. En su camino volverá a pasar el equilibrio y volverá al fondo. Llamamos a esto un ciclo y siempre está hecho de 4 partes. Si comenzáramos desde el equilibrio y la masa subiera, el ciclo no sería cuando volviera por primera vez sino por segunda vez. La masa va desde el equilibrio hacia arriba, vuelve, lo pasa, desciende y luego vuelve al equilibrio.
El tiempo para que la masa complete un ciclo se denomina PERIODO
Como el tiempo se mide en segundos, las unidades para el período también son segundos y usamos la letra mayúscula T como su símbolo. Si cambiamos esa definición y nos preguntamos cuántos ciclos tienen lugar en un período de tiempo, entonces tenemos una frecuencia. Marcamos la frecuencia con f y la medimos en Herz . Aquí está la relación entre el período y la frecuencia:
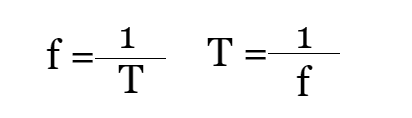
Como el tiempo se mide en segundos, las unidades para el período también son segundos y usamos la letra mayúscula T como su símbolo. Si cambiamos esa definición y nos preguntamos cuántos ciclos tienen lugar en un período de tiempo, entonces tenemos una frecuencia. Marcamos la frecuencia con f y la medimos en Herz . Aquí está la relación entre el período y la frecuencia:.
La amplitud es el desplazamiento máximo
de un objeto desde su posición de equilibrio

Como ya dijimos algunas cosas básicas sobre la masa en un resorte, este es un buen momento para presentarnos al oscilador armónico simple. Consiste en un peso unido a un extremo de un resorte, mientras que el otro extremo está conectado a un soporte rígido. Cuando el sistema se deja en reposo en la posición de equilibrio, entonces la fuerza neta que actúa sobre la masa es cero. Si la masa se desplaza desde la posición de equilibrio, el resorte ejerce una fuerza elástica de restauración que obedece la ley de Hooke.
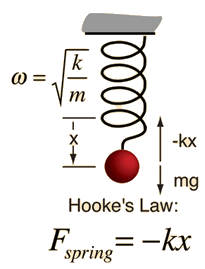
La ley de Hooke establece cómo la fuerza (F) necesaria para extender o comprimir un muelle por distancia x escala linealmente con respecto a esa distancia. Esa fuerza siempre tiene la dirección opuesta al movimiento y al desplazamiento x porque cuando el resorte se comprime, la fuerza desea extenderlo y cuando se extiende, quiere comprimirlo. La fuerza tiende a restablecer el equilibrio del sistema. Esta es la explicación para el signo menos en la fórmula: F = -kx
F (en Newton) en esa fórmula es la fuerza de restauración, x es el desplazamiento (en metros) y k es la constante de resorte (N · m-1) que depende del material del que está hecho el resorte.
Veamos todo el movimiento
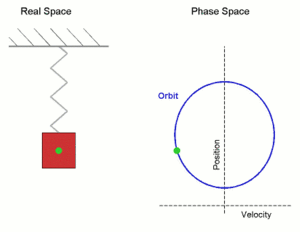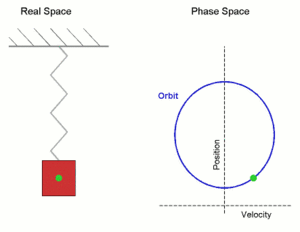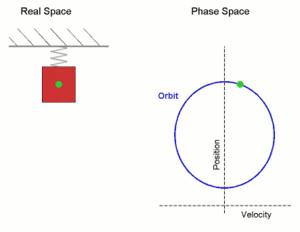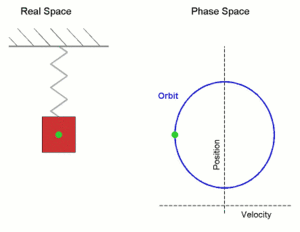
Cuando ponemos una masa en un resorte y el sistema está en reposo, la masa está en la posición de equilibrio. La fuerza neta es cero porque la fuerza del resorte es igual a mg que está tirando de la masa hacia el suelo. Cuando desplazamos la masa de su posición de equilibrio y la dejamos ir, experimenta una fuerza restauradora neta. La masa se mueve hacia la posición de equilibrio. Cuanto más cerca de la masa llega al equilibrio, más pequeña es la fuerza de restauración hasta que se convierte en cero en la posición de equilibrio. La aceleración es cero antes de que la masa comience a moverse desde el fondo, pero es la más alta tan pronto como la dejamos ir y ese es el punto de partida de este movimiento. La aceleración está disminuyendo cuanto más cerca está la masa del equilibrio donde su valor es cero.
En el equilibrio, la masa tiene impulso y continúa moviéndose hacia arriba mientras el resorte se comprime. A medida que el resorte se comprime, la aceleración aumenta. La fuerza de restauración disminuye la masa hasta que se detiene en la posición de amplitud donde la aceleración alcanza su valor más alto nuevamente y la masa comienza a moverse hacia abajo mientras la aceleración disminuye nuevamente hasta que alcanza el valor cero en el equilibrio nuevamente. Cuando la masa pasa el equilibrio, comienza a disminuir la velocidad hasta que alcanza la amplitud inferior desde donde comenzó. Si no hay pérdida de energía, este movimiento se repetirá y tenemos un oscilador armónico simple con movimiento armónico. Como hay una pérdida de energía debido a la amortiguación, la amplitud se acortará más y más con el tiempo hasta que finalmente se vuelva cero y el movimiento se detenga.
¿Qué hay de la energía?
Si recuerdas que un cuerpo tiene energía potencial cuando está en reposo y energía cinética cuando tiene velocidad, comprenderás fácilmente lo que sucede con la energía en este movimiento que describimos. Echemos un vistazo al gráfico.
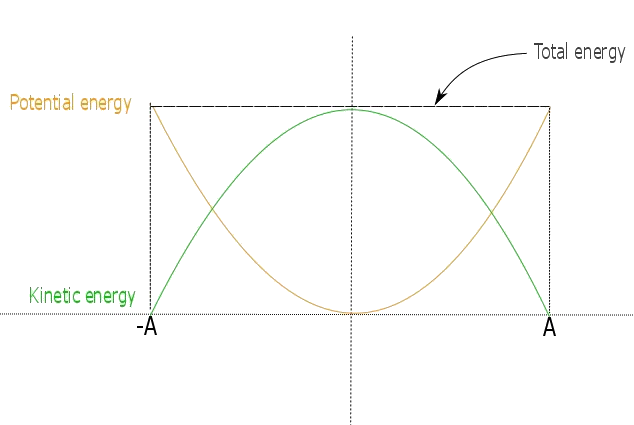
Tenga en cuenta que la energía total es siempre la suma de energías cinéticas y potenciales. Comenzamos en la posición de amplitud donde el cuerpo está en reposo antes de que lo hayamos soltado. Como está en reposo, no hay energía cinética y toda la energía es potencial. Cuando el cuerpo comienza a moverse, su energía potencial disminuye y la cinética aumenta a medida que va recogiendo más y más velocidad. En la posición de equilibrio, la energía potencial es cero y toda la energía es cinética. Cuando el cuerpo continúa moviéndose a la amplitud superior, esa energía cinética está disminuyendo y el potencial aumenta hasta la posición de amplitud donde no hay cinética y toda la energía es potencial. Creo que es hora de revisar lo que hemos cubierto hasta ahora...
| Posición | Energía | Aceleración | Fuerza | Velocidad |
|---|---|---|---|---|
| Baja amplitud | POTENCIAL | máximo | máximo | cero |
| Equilibrio | KINETIC | cero | cero | máximo |
| Amplitud superior | POTENCIAL | máximo | máximo | cero |
Como puede ver, el desplazamiento, la velocidad y la aceleración son periódicos. Podemos resolver ecuaciones diferenciales para obtener funciones de solución. Esas funciones son trigonométricas. Si esto es demasiado para ti, no me importaría si te desplazas por esta parte. :)
| Cantidad física | Función de solución |
|---|---|
| desplazamiento | x = cos(ωt) |
| Velocidad | v = -Aωsin(ωt) |
| aceleración | a = -Aωωcos(ωt) |
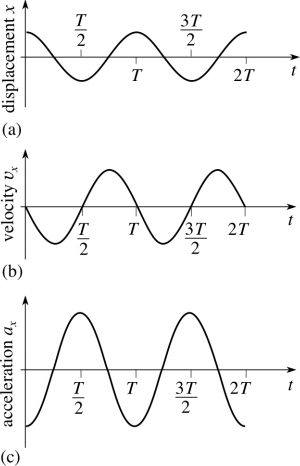
Esas son soluciones a ecuaciones diferenciales y ω = 2πf es la frecuencia angular. Podemos ver los gráficos de esas funciones y observar cómo se puede explicar todo con solo mirarlas.
Como se puede ver en estos gráficos, el desplazamiento comienza desde la amplitud, la velocidad desde cero porque allí es cero y la aceleración desde su valor máximo. Las funciones son periódicas y cambian de una manera que ya explicamos.
Ahora nos estamos moviendo a una pregunta importante con respecto al período y la frecuencia. ¿De qué dependen? ¿Cambiará el movimiento si cambiamos la masa o cambiará si tenemos la misma masa pero aumentamos la amplitud?
El período y la frecuencia son independientes de la amplitud
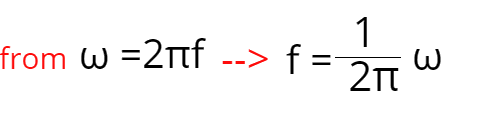
No importa si tira esa masa hacia abajo en un par de centímetros o en un metro, el período y la frecuencia serán los mismos. Veamos por qué es eso. Sabemos que el momento angular es ω = 2πf y también sabemos que el momento angular depende de la masa y la constante de resorte que se muestra con estas fórmulas:
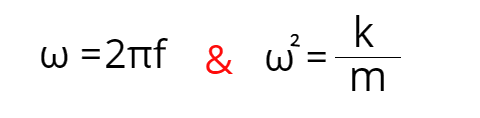
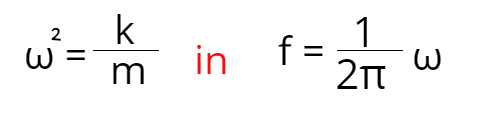
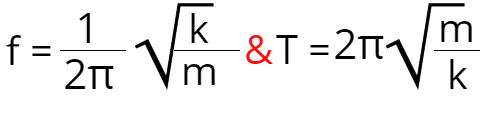


Como dije al principio, para que suene primero tenemos que hablar de las ondas y para comenzar a hablar sobre las ondas necesitamos vibración. En esta publicación Física explicada hemos cubierto la vibración y todo lo que necesitaremos con respecto al movimiento armónico desde el desplazamiento y la aceleración hasta las energías y la frecuencia. Sé paciente, las olas llegarán pronto, ¿estás preparado para ellas? Hasta la próxima vez
MANTENGA SU SONRISA
RESPETE TU GENIO INTERIOR!

Para obtener más información sobre este tema, asegúrese de consultar estos recursos:
Simple harmonic motion
Vibrational motion
Vibration
Periodic motion
Hooke's law
Harmonic motion
Fuentes de imagen:
La imagen gif de la masa en un resorte es de wiki y se puede encontrar Aquí
- la imagen de portada es de pngtree y está libre de royalties, se puede encontrar Aquí
- clipart en mis títulos es de pixabay y se ubican Aquí
- masa roja en primavera es de hyperphysics.phy y se encuentra Aquí
- el espacio real y el gif del espacio de fase es de wiki y esta Aquí
- el gráfico con energías es del Movimiento Periódico. Brilliant.org. Consultado 08:25, 25 de julio de 2018, en https://brilliant.org/wiki/identifying-periodic-motion/
- 3 gráficos son de physics.brocku y son Estos
- reloj de péndulo es de wiki y esta es su fuente Aquí
- todas las otras imágenes con ecuaciones las hice yo mismo

Thanks for Past support on my Post.
|| @utopian-io || @anomadsoul || @acidyo || @ocd-resteem || @steemstem || @vortac || @cervantes || @hendrikdegrote || ¡Vote for theres as witness! Here: https://steemit.com/~witnesses



La imagen gif de la masa en un resorte es de wiki y se puede encontrar Aquí
- la imagen de portada es de pngtree y está libre de royalties, se puede encontrar Aquí
- clipart en mis títulos es de pixabay y se ubican Aquí
- masa roja en primavera es de hyperphysics.phy y se encuentra Aquí
- el espacio real y el gif del espacio de fase es de wiki y esta Aquí
- el gráfico con energías es del Movimiento Periódico. Brilliant.org. Consultado 08:25, 25 de julio de 2018, en https://brilliant.org/wiki/identifying-periodic-motion/
- 3 gráficos son de physics.brocku y son Estos
- reloj de péndulo es de wiki y esta es su fuente Aquí
- todas las otras imágenes con ecuaciones las hice yo mismo
|| @utopian-io || @anomadsoul || @acidyo || @ocd-resteem || @steemstem || @vortac || @cervantes || @hendrikdegrote || ¡Vote for theres as witness! Here: https://steemit.com/~witnesses


Cada dia haces de tu contenido una verdadera obra de arte @caracasfrases mis respetos!!
Que bella mi amiga !! Gracias !!
interesante amigo!! me hicistes recordar cuando estudie esas fórmulas y estos temas en ingeniería!! tiempos aquellos de estudiante...ya llevo 15 años de egresada, como pasa el tiempo... Soy Ingeniera Mecánica... Saludos Amigo!!
Otra ingeniera por aquí
!! interesante !!
si me hubieses dado clases de física no me hubiese resultado tan tediosa esa asignatura, jeje, saludos
jajaja ah tu ves.....