Aprendiendo de Vectores / Ejercicios , Consejos / Para los amantes del saber
El dia de hoy aprenderemos Vectores fuerzas ; cómo sumar fuerzas y resolverlas en componentes usando la ley del paralelogramo , expresar la fuerza y la posición en forma vectorial cartesiana y explicar cómo determinar la magnitud y el sentido del vector
Vectores Fuerzas
Una fuerza representa la acción de un cuerpo sobre otro y se caracteriza por su punto de aplicación, magnitud o módulo y dirección.Un vector se representa gráficamente por medio de una flecha, la cual se usa para definir su magnitud, dirección y sentido.
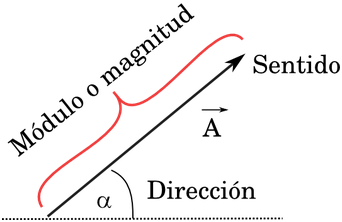
Magnitud: es la medida que hay desde la cola del vector hasta la flecha del vector o punta.
Dirección: es la inclinación que posee el vector fuerza con una línea horizontal o con una línea vertical.
Sentido: lo da la flecha o punta del vector fuerza.
Tipos de Vectores
Vector Fijó: como su nombre lo representa es un vector que no se mueve , está situado en punto concreto.

Vector Deslizante: es aquel vector que puede desplazarse en línea recta.
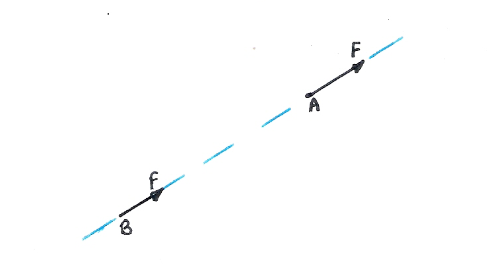
Vector libre: es aquel vector que puede moverse en cualquier espacio.
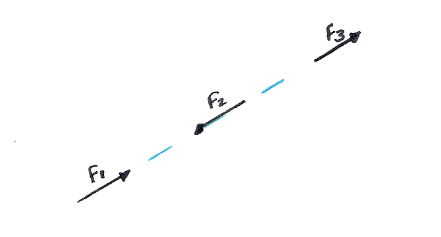
Vector colineales : se trata de aquellos que aparecen en la misma recta o que resultan paralelos a una cierta recta.Cuando las relaciones que mantienen sus coordenadas son iguales y el producto vectorial es equivalente a 0, dos vectores son colineales.
Vectores opuestos: son aquellos que tienen la misma dirección y la misma magnitud, pero cuentan con sentidos contrarios.

Vectores concurrentes : a aquellos que atraviesan un mismo punto. Debido a que, al pasar por dicho punto dan lugar a la creación de un ángulo, los vectores concurrentes también se denominan vectores angulares.
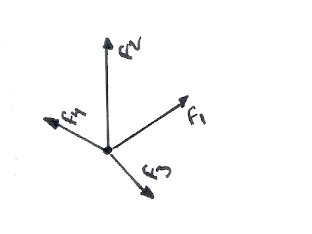
Vectores iguales : son aquellos que tiene igual magnitud , igual dirección e igual sentido.
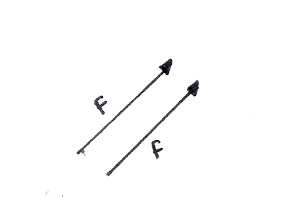
Vectores coplanares son los que están en un mismo plano.
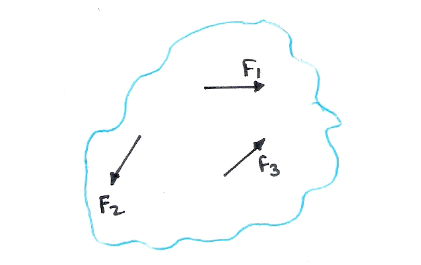
Existen operaciones básicas con vectores
Suma de vectores: Dos vectores A y B , tal como los de fuerza o posición en la imagen numero 1 pueden sumarse para formar un vector “ resultante “ R= A+B usando la ley de paralelogramo. También se puede sumar B a A usando una construcción triangular, un caso especial de la ley del paralelogramo, en donde el vector B se suma al vector A en forma de “ cabeza a cola “ , eso es conectado a la cabeza A a la cola B.
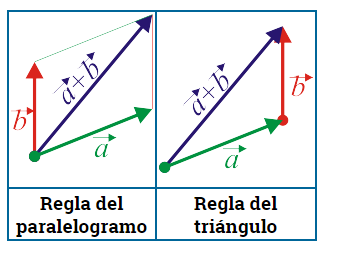
Conmutativa

Asociativa
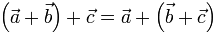

Resta de Vectores: la diferencia entre dos vectores A y B del mismo tipo puede ser expresada como
Esta suma vectorial se muestra gráficamente en la figura B, dado que la resta se define como un caso especial de la suma, las reglas de la suma vectorial también se aplican a la resta vectorial.
Procedimiento de análisis
Los problemas que implican la suma de dos fuerza pueden resolverse de la siguiente manera :
Ley del paralelogramo.
1-Trace un croquis mostrando la adición vectorial usando con la ley del paralelogramo.
2-Dos fuerzas componentes se suman de acuerdo con la ley del paralelogramo, Produciendo una fuerza resultante que forma la diagonal del paralelogramo.
3-Si una fuerza debe resolverse en componentes a lo largo de dos ejes dirigidos desde la cola de la fuerza, entonces comience en la cabeza de la fuerza y construya líneas paralelas a los ejes , formando así el paralelogramo.
4 –Marque todas las magnitudes de fuerzas conocidas y desconocidas y los ángulos sobre el croquis e identifique la dos incógnitas.
Tips para trigonometría
1-Trace de nuevo media porción del paralelogramo para ilustrar la adicción triangular cabeza a cola de las componentes.
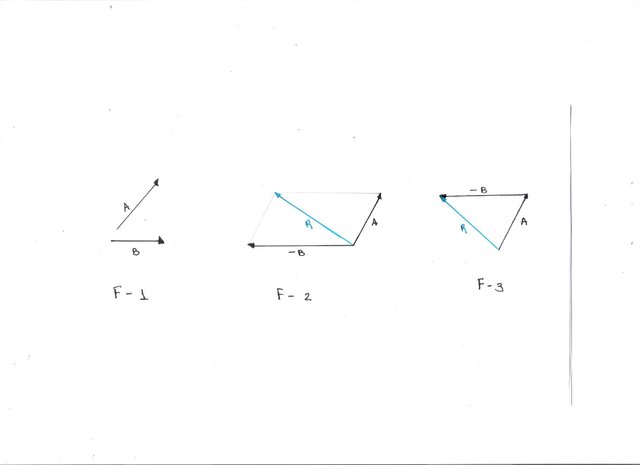
2- La magnitud de la fuerza resultante puede ser determinada con la ley de los cosenos y sus direcciones mediante la ley de los senos.

Nota
Puntos importantes
*Un escalar es un número positivo o negativo.
*Un vector es una cantidad que tiene magnitud, dirección y sentido.
*La multiplicación o la división de un vector por, o entre un escalar cambiara la magnitud del vector. El sentido del vector cambiara si el escalar es negativo.
*Como un caso especial, si los vectores son colineales , la resultante se obtiene con una suma algebraica o escalar.
Ejercicios
Determiné la magnitud de la fuerza resultante de F1 y F2 y su dirección medida de sentido contrario de las agujas del reloj con respecto al eje
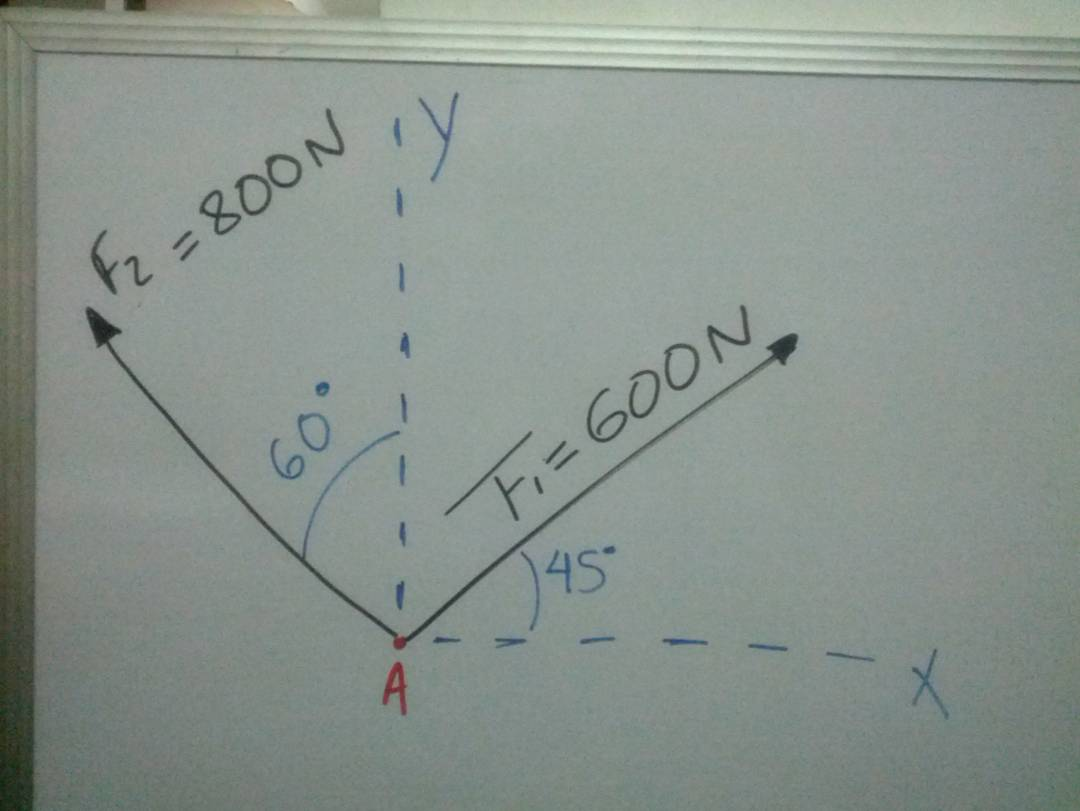

Primer paso es hacer un Diagrama de cuerpo libre , identificando lo que tenemos para hacer más fácil el ejercicio , para saber que tengo y que tengo que buscar .
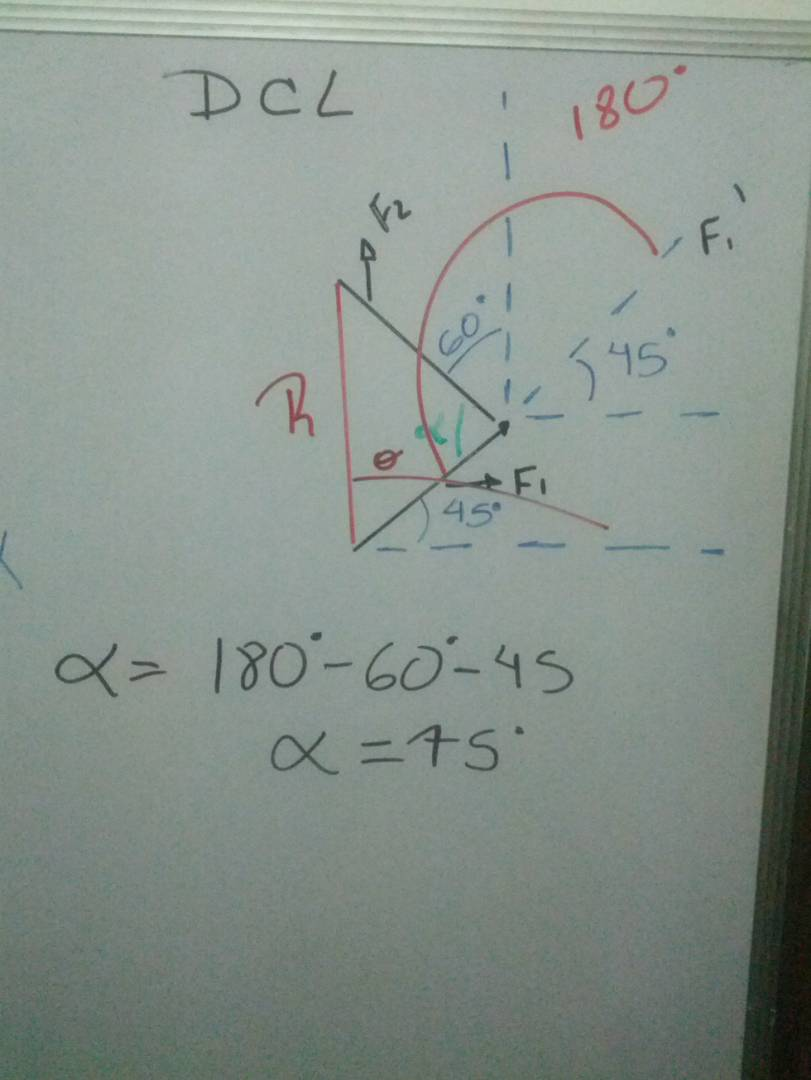
Nuestra incógnitas son tita y alfa, se puede observar que la misma línea de tita es la mitad de una circunferencia entonces es 180 º , entonces sabiendo eso busco el valor de alfa restando 180-45-60 para obtener el valor de alfa.
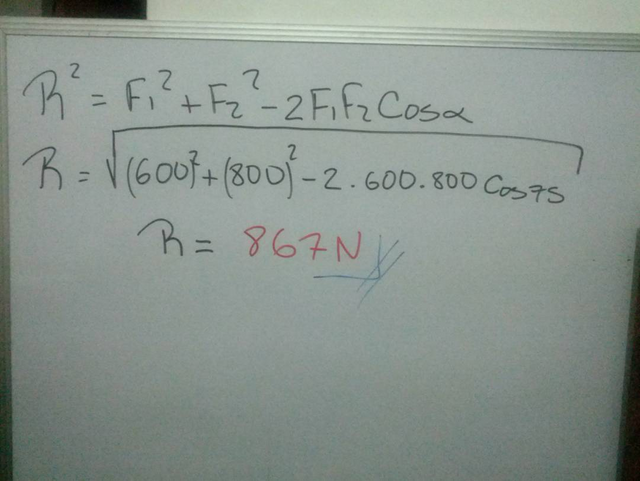
Aplicamos ley de cosenos ya que tenemos todas nuestra incógnitas que era f1, f2 y el ángulo de f1 y f2.
Bibliografia
Mecanica Vectorial para ingenieros décima edición estatica beer,Jhonston,Mazurek
Mecanica Vectorial para ingenieros Estatica Russel C . Hibbeler
https://definicion.de/vectores-colineales/.
https://definicion.de/vectores-concurrentes/
https://es.wikipedia.org/wiki/Teorema_de_los_senos
https://es.wikipedia.org/wiki/Teorema_del_coseno
Espero que le haya gustado esta explicación de Vectores , nos vemos en los próximos post donde compartiré con ustedes algunos conocimientos de la mecánica , si tiene duda o un ejercicios que quiere que realice respecto a mecánica escribanme . Gracias por leer .

Que locura men pero muy bien explicado!!
Gracias men , que bien que te gusto !
Muy buena explicación gracias por tu abanico de posibilidades para aprender
que bueno que te gusto amigo !
Esto me recuerda mis años en la universidad, bien explicado compañero. Saludos!!!
si esto es lo básico que aprendes en la uni amigo , que bueno que te gusto
Gracias por tu aporte, es necesario que steemit también cumpla su misión didáctica, muy post , completo , argumentado, bien explicado... El equipo Cervantes apoyando el contenido de calidad.
Gracias a el equipo de cervantes !
Buena info amigo !!! Refrescando conceptos
Asi es amigo