Fundamentos físicos y matemáticos de las leyes de Kirchhoff (Simulación y demostración experimental)
¡Hola amigos de Steemit!
Reciban un cordial saludo.
Los análisis de redes eléctricas, sistemas electrónicos y sistemas de telecomunicaciones han sido fundamentales en el desarrollo y avance de un gran número de tecnologías, en las que los principios físicos y modelos matemáticos desarrollados por décadas por grandes científicos han sido el pilar de estos logros.
En este artículo desarrollaré un análisis teórico y experimental de las leyes que hasta la fecha ocupan un lugar privilegiado en el análisis de estos sistemas:
Las leyes de Kirchhoff
Dada la importancia que ha significado el uso de estas leyes en el análisis de sistemas, desde los más simples hasta los más complejos, profundizaremos en los principios físicos y matemáticos que soportan dichas leyes con el objeto de contribuir en la consolidación de nuestros conocimientos en lo que ha sido una de las herramientas de análisis de gran impacto en la solución de una gran variedad de sistemas.
Fundamentos teóricos
Debido a que las leyes de Kirchhoff están asociadas a las diferencias de potencial y las corrientes eléctricas de una red, haremos a continuación una descripción de estos parámetros los cuales están íntimamente ligados al principio de conservación de la energía y el principio de conservación de la carga.
Ley Kirchhoff de los voltajes
En la figura 1 se muestra una carga eléctrica “q0” que se desplaza entre dos puntos A y B en presencia de un campo eléctrico “E” el cual consideramos de tipo estacionario.
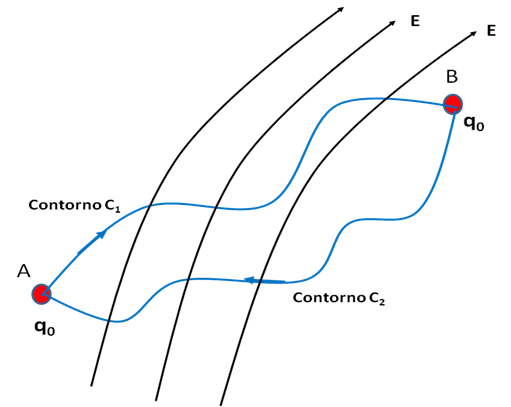
en presencia de un campo eléctrico estacionario
(Elaboración propia)
Este desplazamiento de la carga entre dichos puntos implica que esta experimente una diferencia de potencial "∆V" definida por la siguiente expresión:
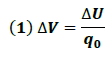
Donde "∆U" representa la variación de la energía potencial entre los dos puntos.
Del principio de conservación de la energía en ausencia de fuerzas disipativas sabemos que el trabajo y la variación de la energía potencial están relacionados según la ecuación:
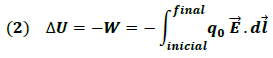
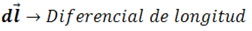
La sustitución de (2) en (1) nos conduce a la siguiente expresión:
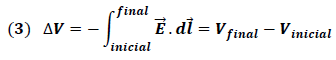
De esta forma se aprecia que si el desplazamiento de la carga es en una trayectoria cerrada, donde la carga inicia y termina en un mismo punto como el observado en la figura 1, la diferencia potencial es nula.
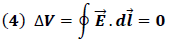
Donde el símbolo en la integral denota un camino cerrado.
Ahora consideremos el caso de un conductor de resistencia “R” sometido a un campo eléctrico el cual es gobernado por la ley de Ohm.
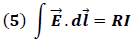
Si el campo que se aplica es estacionario y el conductor es cerrado el termino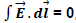 
, lo cual implica I = 0.
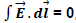, lo cual implica I = 0.
Este hecho pone de manifiesto que para establecer una corriente eléctrica en un circuito, es imperativo la aplicación de una fuerza electromotriz a través de generadores eléctricos o por métodos de inducción que garantice el flujo de cargas en el circuito cerrado.
En la figura 2 se ilustra el caso de una trayectoria o lazo cerrado también conocida como malla donde la aplicación de la ecuación (4) toma la forma:
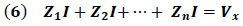
Donde el termino "ZnI" representa según, la ley de Ohm, el voltaje de cada uno de los elementos con una impedancia "Zn".
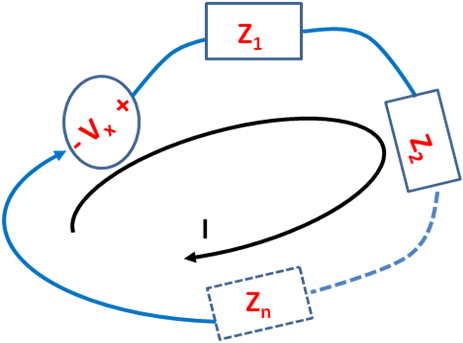
(Elaboración propia)
En la expresión (6) se observa que de no existir un generador “Vx” la corriente eléctrica se anularía a no ser que un campo magnético variable induzca una corriente eléctrica en dicho circuito, tal y como lo establece la ley de Faraday.
La expresión (6) puede escribirse de la forma:
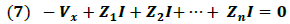
La ecuación (7) es conocida como la ley de Kirchhoff de los Voltajes y es escrita en general de la forma:
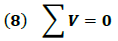
Ley de Kirchhoff de las corrientes
En la figura (3) se muestra una distribución de carga volumétrica “ρv” encerrada en un volumen el cual es definido por una superficie cerrada.
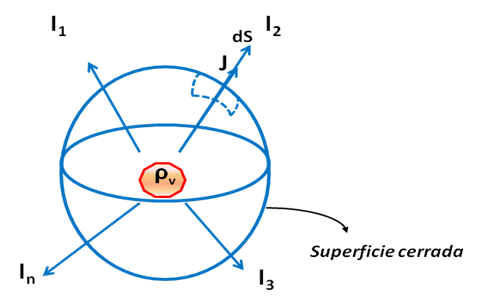
(Elaboración propia)
Por definición el flujo de carga o corriente eléctrica está dado por la expresión:
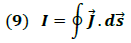
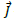→ Densidad superficial de corriente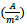 
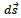→ Diferencial de superficie (m2 )
Para simplificar el análisis consideremos el caso en el que la carga eléctrica “Q” decrece mientras fluye hacia el exterior de la región acotada por la superficie esférica.
Según el principio de conservación de la carga, la ecuación (9) puede expresarse como:
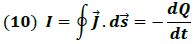( flujo de carga que decrece)La expresión (10) es equivalente a la ecuación de continuidad la cual se escribe:
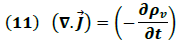
Dado que en el caso de corrientes estacionarias la densidad de carga no presenta variación temporal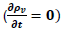 
, la ecuación (11) nos conduce a una divergencia nula según se expresa en la siguiente ecuación:
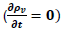, la ecuación (11) nos conduce a una divergencia nula según se expresa en la siguiente ecuación: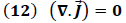
De esta forma relacionando (10) y (11) a través del teorema de la Divergencia el cual establece que:
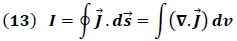
Obtenemos:
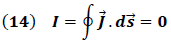
La expresión (14) es extensiva a cada una de las contribuciones de flujo que atraviesan dicha superficie.
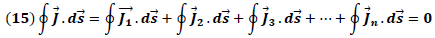
Cada uno de los términos en la expresión (15) representa los flujos de carga o corrientes eléctricas que fluyen al exterior de la superficie por lo que podemos escribir esta ecuación de la forma:
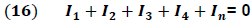
La expresión (16) es conocida como la ley de Kirchhoff de las corrientes y es escrita en general de la forma:
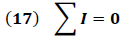
Una forma práctica de escribir la ley de Kirchhoff de las corrientes es mostrada en la expresión (18), donde según el principio de conservación de la carga el flujo de entrada en un punto (nodo) debe ser igual al flujo de salida.
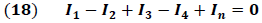
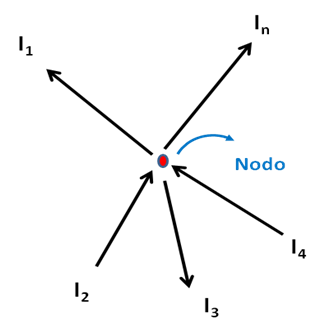
(Elaboración propia)
En la siguiente fase de este artículo realizaremos una simulación y un pequeño ensayo experimental con el objeto de demostrar la validez de las leyes de Kirchhoff.
Parte experimental
En la siguiente imagen se muestra un circuito eléctrico simulado con el software para circuitos eléctricos Proteus.
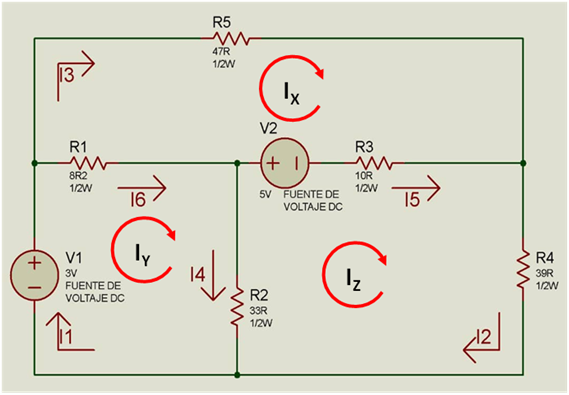
Cada malla (circuito cerrado) o nodo (punto de amarre de dos o más elementos) es gobernado por las leyes de los voltajes y corriente respectivamente.
Si bien existen una gran variedad de técnicas de análisis de redes derivadas de las leyes de Kirchhoff, la ley de los voltajes aplicada en las mallas principales es la forma más simple de resolver el sistema. Las mallas principales están identificadas en nuestro caso por las corrientes de malla Ix, Iy, y Iz.
Cada ecuación es obtenida realizando un recorrido a través de la malla seleccionada, registrando cada uno de los voltajes hallados en dicho recorrido. Este recorrido se inicia en uno de los nodo de la malla y se completa una vez se retorne al nodo de partida. Una condición que no se debe violar en dicho recorrido es pasar por un nodo más de una vez.
Cálculos y resultados teóricos
La ley de los voltajes aplicada en cada malla del circuito nos conduce al siguiente sistema de ecuaciones:
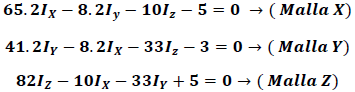
La solución del sistema de Ecuaciones arroja los siguientes valores para las corrientes de malla:
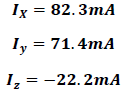
Es importante resaltar que las corrientes de malla deben asociarse a las corrientes en los conductores según se muestra a continuación:
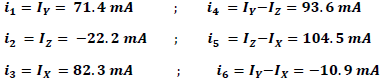
Voltajes obtenidos en cada resistencia según la ley de Ohm
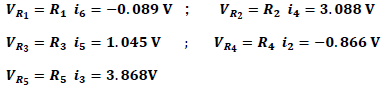
Valores de corriente y voltaje en cada elemento según el simulador
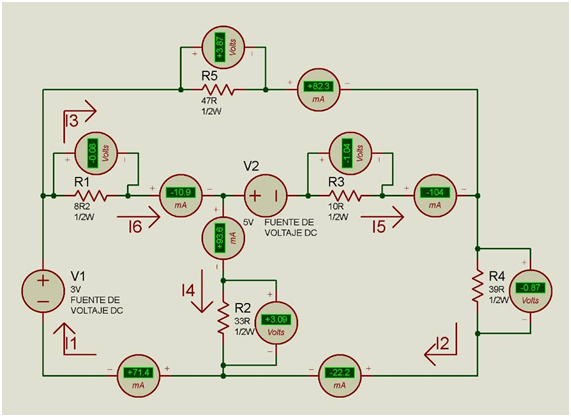
En las siguientes imágenes se muestra el ensayo experimental del circuito realizado en el laboratorio de prueba.
De esta forma podemos apreciar que la concordancia entre los valores teóricos y los resultados obtenidos con el software de simulación y la verificación experimental, demuestran la validez de las leyes de Kirchhoff, soportada en los fundamentos físicos y matemáticos aquí expuestos.
Con esto concluyo esta publicación, esperando que la información compartida permita afianzar sus conocimientos sobre los conceptos básicos de electromagnetismo y sus aplicaciones en redes eléctricas. Si tienes alguna pregunta, duda o sugerencia, deja tu comentario y con mucho gusto te responderé.
Gracias por leer mi publicación.
Referencias
- Circuitos Eléctricos. James W. Nilson. Cuarta edición. Addison-Wesley Iberoamericana.
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Electrodinamica Clasica Segunda Edición / John David Jackson.
- Electromagnetismo Conceptos y Aplicaciones Cuarta Edición / Stanley V. Marshall, Richard E. DuBroff, Gabriel G. Skitek.
- Física Vol. II Campos y ondas. Marcelo Alonso, Edward J. Finn. Fondo Educativo Interamericano, S.A.
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.
Hola @yaribel. Gracias por la visita y el comentario. saludos
Tema fundamental en la física, el mundo eta rodeado de un sinfín de aplicaciones y es fascinante que expliques de donde proviene todo, diferentes aparatos eléctricos y electrónicos necesitan de circuitos para su funcionamiento, no se mucho de este tema pero me encanta leer este tipo de publicaciones
saludos @anaestrada12. Gracias por la lectura y el apoyo. Ciertamente los conceptos físicos sus orígenes y aplicaciones son fascinantes. Gracias por la visita.
Saludos @lorenzor, buena exposición sobre el tema. Casi siempre quedan en el aire temas como este. Lo voy a re-esteemear...
Mis saludos @jfermin70. Gracias por la lectura y el tiempo dedicado. Me alegra le gustara el tema y la presentación. Agradecido por el apoyo.
Muy bueno el trabajo estimado @lorenzor. La correlación de la teoría y la práctica es la base de un aprendizaje significativo. Saludos!
Saludos @emiliomoron. Es un gran apoyo para fortalecer los fundamentos teóricos la puesta en practica de lo aprendido. gracias por el apoyo
Muy buena enseñanza nada como aprender haciendo, es decir ir de la teoria a la explicación o vivencia prática interesante post @lorenzor
Hola @yekamendez. La experimentación nos fortalece el conocimiento teórico. gracias por la lectura y apoyo.
La parte experimental de montar los circuitos eléctricos para demostrar la Ley de Kirchhoff de los voltajes y la Ley de Kirchhoff de la corriente es sencillamente una manera directa y muy didáctica de plantear un tema de Física muy importante para los estudiantes de ciencias e ingeniería, te felicito
Saludos @azulear. Las demostraciones experimentales con los equipos que contamos actualmente son una herramienta valiosa para alcanzar nuestros objetivos. Gracias por el apoyo y comentario.
Hermano @lorenzor. Extraordinario trabajo sobre las famosas Leyes de Kirchhoff. Muy bien presentado y didáctico, mis felicitaciones. Un abrazo.
Mi estimado @tsoldovieri. Saludos . Es grato tenerlo por aquí de visita. Gracias por la lectura y apoyo.