¡Hola amigos de Steemit!
Reciban un cordial saludo.
Los fundamentos electromagnéticos en los que se basa el funcionamiento de una gran variedad de dispositivos han permitido la creación de tecnologías de vanguardia que han contribuido significativamente en el desarrollo de nuestras vidas. Los osciladores electromagnéticos son uno de los ejemplos donde estos principios juegan un rol fundamental.
Dada su importancia, en esta publicación realizaremos un análisis teórico y experimental de un oscilador electromagnético cuyas aplicaciones son de gran interés en distintas áreas de la ingeniería.
Fundamentos teóricos
Si bien existen una gran variedad de osciladores electromagnéticos, concentraremos nuestro análisis en un modelo simple constituido por un capacitor, un inductor y una resistencia combinados en serie, cuyos resultados pueden ser extendidos a modelos más complejos.
Oscilación sin amortiguamiento (Caso ideal)
En la siguiente imagen se muestra un circuito simple conformado por un capacitor y un inductor en el que la resistencia ofrecida por el circuito se considera despreciable.
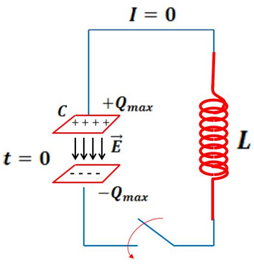 Figura 1. Circuito L-C
Figura 1. Circuito L-C
(Elaborada por @lorenzor en Microsoft Powerpoint)
En la Figura 1 el capacitor, previamente cargado (t=0), contiene toda la energía del circuito debido a la carga eléctrica acumulada en sus placas, según lo establece la siguiente expresión:
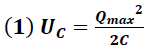 Energía de un capacitor
Energía de un capacitor
Qmax → Carga máxima en la placa del capacitor (c)
C → Capacitancia (f)
En el instante que el interruptor se cierra, la carga fluye a través del circuito estableciéndose una corriente eléctrica que energiza al inductor.
En la medida que el capacitor se descarga, la energía es transferida y almacenada en su totalidad en el campo magnético del inductor, según lo expresa la siguiente ecuación:
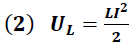 Energía de un Inductor
Energía de un Inductor
L → Inductancia (H)
I → Corriente eléctrica (A)
Este proceso oscilatorio de transferencia de energía eléctrica y magnética entre el capacitor y el inductor se mantiene indefinidamente debido a que la disipación de la energía es nula en un sistema donde la resistencia ofrecida por el circuito es cero.
Ahora bien, la energía total del circuito "U" en cualquier tiempo “t” está dada por la suma de la energía del capacitor y el inductor según lo muestra la siguiente expresión:
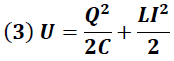
Dado que la energía del sistema permanece constante, su variación temporal debe ser nula, por lo que se debe cumplir la siguiente condición:
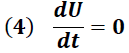
Derivando la ecuación (3) y considerando lo establecido por la ecuación (4) se tiene:
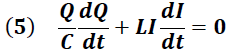
Por definición la corriente eléctrica está dada por la expresión:
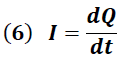
Derivando la ecuación (6) obtenemos:
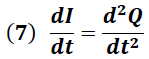
Sustituyendo (6) y (7) en (5) se obtiene:
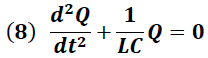
La ecuación diferencial dada por la expresión (8), es representativa del movimiento oscilatorio que experimenta la carga eléctrica en el circuito y tiene como solución la siguiente expresión:
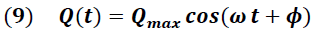
Donde “ω" representa la frecuencia natural angular de la oscilación y está dada por la expresión:
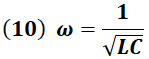
ϕ → constante de fase
En la siguiente imagen se visualiza el proceso oscilatorio de la transferencia de energía entre el capacitor y el inductor.
.gif) Figura 2. Visualización de la oscilación en el circuito L-C
Figura 2. Visualización de la oscilación en el circuito L-C
Wikipedia con licencia Creative Commons CC0 1.0 Universal Public Domain Dedication
Oscilación amortiguada
En un sistema donde la energía es disipada en forma de calor debido a la presencia de una resistencia, tal y como se muestra en figura 3, es imperativo reformular el proceso oscilatorio bajo esta nueva variable.
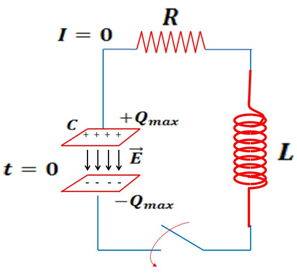 Figura 3. Circuito oscilante R-L-C
Figura 3. Circuito oscilante R-L-C
(Elaborado por @lorenzor en Microsoft Powerpoint)
Dado que la energía es disipada por el sistema, la expresión (4) toma la forma:
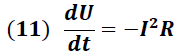
Donde "I2 R" representa el valor de la energía disipada debido a la resistencia.
De esta forma la variación temporal de la energía total del sistema dada por la expresión (3) toma la forma:
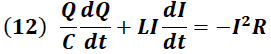
Sustituyendo (6) y (7) en (12) se obtiene:
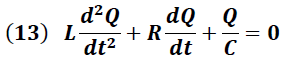
La solución de la ecuación (13) está dada por la expresión:
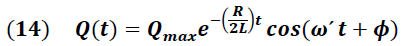
Donde "ω´" representa la frecuencia angular con amortiguamiento.
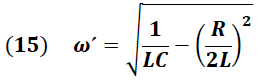
En los sistemas amortiguados, el valor de la resistencia determina el tipo de oscilación que experimenta el sistema.
La frecuencia angular dada por la ecuación (15), permite analizar el tipo de oscilación que se obtiene de acuerdo al valor de la resistencia que el sistema ofrece, de la que se desprenden los siguientes casos:

En la siguiente representación grafica se visualiza el comportamiento de la oscilación eléctrica amortiguada según el valor de la resistencia del sistema.
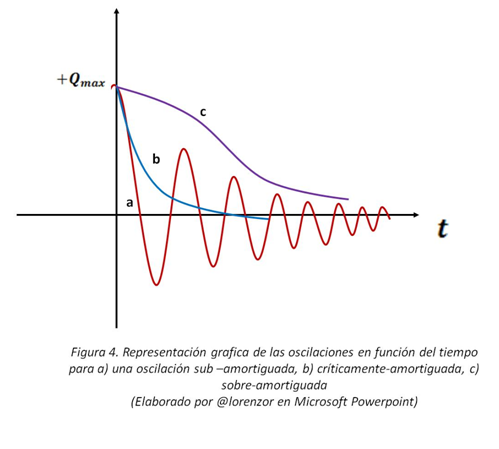
Es importante destacar que las oscilaciones eléctricas aquí expuestas son análogas a las oscilaciones que experimentan los sistemas mecánicos, como es el caso de un sistema masa–resorte.
En la siguiente figura se ilustra la analogía existente entre las oscilaciones mecánicas y las oscilaciones eléctricas.
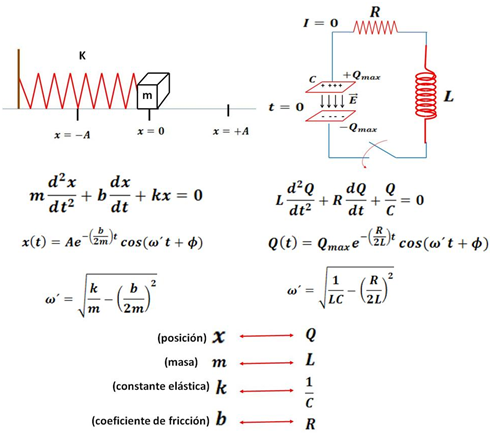 Figura 5. Analogía entre los sistemas oscilantes mecánicos y eléctricos.
Figura 5. Analogía entre los sistemas oscilantes mecánicos y eléctricos.
(Elaborado por @lorenzor en Microsoft Powerpoint)
Estas analogías son de gran utilidad en el análisis de sistemas dinámicos complejos, ya que la transformación de estos sistemas dinámicos a sistemas análogos eléctricos permite la obtención de soluciones a través de técnicas de análisis de circuitos significativamente más simples.
Demostración experimental de una oscilación sub-amortiguada
En la siguiente imagen se muestra un circuito R-L-C en serie energizado, cuyos parámetros conducen a una oscilación sub-amortiguada.
 Figura 6. Circuito R-L-C en serie
Figura 6. Circuito R-L-C en serie
(Fotografía tomada en el laboratorio por @lorenzor)
Datos y cálculos experimentales

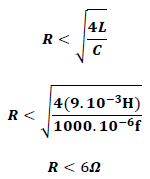
El resultado obtenido muestra que la oscilación amortiguada esta en correspondencia con la condición de una oscilación sub-amortiguada dada por la expresión (16).
En las imágenes que se muestran a continuación se observa el comportamiento oscilatorio sub-amortiguado en el circuito R-L-C.
 Figura 7. Medida de la señal amortiguada en el circuito R-L-C
Figura 7. Medida de la señal amortiguada en el circuito R-L-C
(Fotografía tomada en el laboratorio por @lorenzor)
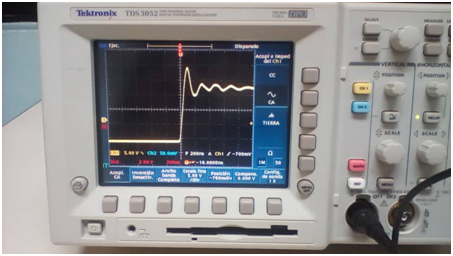 Figura 8. Visualización de la oscilación sub-amortiguada en el circuito R-L-C
Figura 8. Visualización de la oscilación sub-amortiguada en el circuito R-L-C
(Fotografía tomada en el laboratorio por @lorenzor)
Los osciladores eléctricos amortiguados son de gran utilidad en la atenuación o eliminación de señales de ruido o señales oscilantes no deseadas y funcionan además como filtros en distintos rangos de frecuencia, convirtiéndolos en dispositivos versátiles de bajo costo y con una amplia gama de aplicaciones.
Espero este artículo contribuya con el fortalecimiento de sus conocimientos sobre los procesos oscilatorios electromagnéticos. Si tienen alguna pregunta, duda o sugerencia, dejen sus comentarios y con mucho gusto les responderé.
Gracias por leer mi publicación.
Referencias
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Electrodinámica Clásica Segunda Edición / John David Jackson
- Electromagnetismo Conceptos y Aplicaciones Cuarta Edición / Stanley V. Marshall, Richard E. DuBroff, Gabriel G. Skitek
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo II. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 2. Addison Wesley Longman.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.

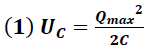 Energía de un capacitor
Energía de un capacitor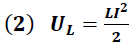 Energía de un Inductor
Energía de un Inductor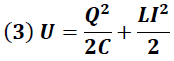
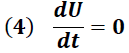
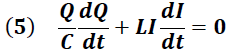
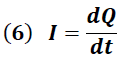
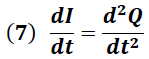
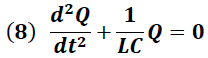
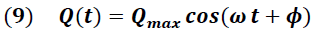
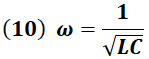
.gif)

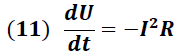
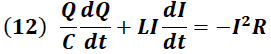
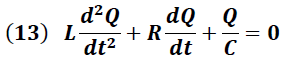
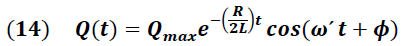
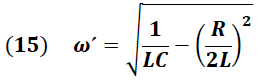





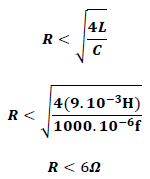


This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Mi agradecimiento por el apoyo.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Buen trabajo @lorenzor, precisamente hoy les explicaba a los Estudiantes de Telecomunicaciones de URU como resolver este tipo de circuitos con Ecuaciones Diferenciales. Les voy a dar tu enlace para lo lean... Un abrazo...
Gracias por la visita y el apoyo mi estimado @jfermin70. Espero le sea útil a sus estudiantes.
Gracias por el apoyo.
Excelente publicación saludos.....
Saludos @felixrodriguez. Gracias por el apoyo.
HOLA @lorenzor, felicitaciones en tu post. Yo tengo un post similar sobre circuitos RCL, midiéndolos con el osciloscopio y la calculadora. Estaba desconectado de steemit por razones tecnológicas. Pero ya estaré activo con un nuevo post.
Saludos @germanmontero. Gracias por su visita y apoyo.
Hi @lorenzor!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Gracias por el apoyo.
Congratulations @lorenzor! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPHello @lorenzor! This is a friendly reminder that you have 3000 Partiko Points unclaimed in your Partiko account!
Partiko is a fast and beautiful mobile app for Steem, and it’s the most popular Steem mobile app out there! Download Partiko using the link below and login using SteemConnect to claim your 3000 Partiko points! You can easily convert them into Steem token!
https://partiko.app/referral/partiko