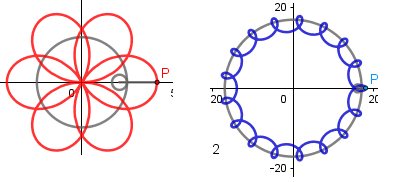
(Todas las imágenes y animaciones han sido hechas por mi usando el software matemático GeoGebra Classic 5.)
Saludos estimados lectores especialmente a los miembros de la comunidad
#stem-espanol, hoy en un nuevo artículo de
Matemática dinámica continuamos explorando el software matemático GeoGebra Classic 5, en esta oportunidad siguiendo con el tema sobre las curvas del tipo ruleta cicloidal y para culminar las simulaciones sobre ellas les traigo la
curva hipocicloide, esta curva al igual que las dos anteriores que hemos simulado se produce por la trayectoria de un punto sobre una circunferencia, lo que la diferencia de las otras dos es que la circunferencia rueda en la parte interna de otra circunferencia al contrario de la epicicloide que lo hace en la parte externa.
Formalmente una curva hipocicloide es
la curva que describe la trayectoria de un punto sobre una circunferencia que rueda sin deslizar en el interior de una circunferencia directriz.
Recordemos que el propósito de esta serie de artículos no es profundizar en el fenómeno simulado sino, a través de la creación de la simulación aprender el funcionamiento del software; si desean más información sobre la curva hipocicloide pueden leer
mi artículo donde hice un estudio detallado de ella.
Si es el primer artículo sobre matemática dinámica que lees te invito a que revises los dos anteriores ya que en ellos se pusieron en práctica herramientas que ya no serán explicadas en el presente.
Artículos anteriores:
Introducción al software.
Construcción de curva epicicloide y caustica.
Ahora sí, empecemos...
Construcción hipocicloide.
Empezaremos escribiendo en la barra de entrada las ecuaciones paramétricas de la epicicloide
Para el eje x:

Para el eje y:

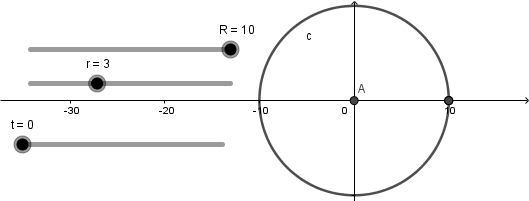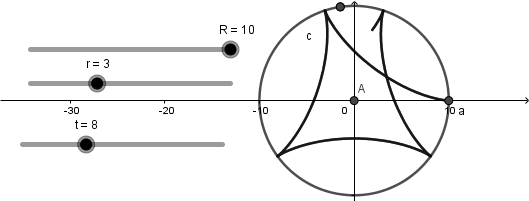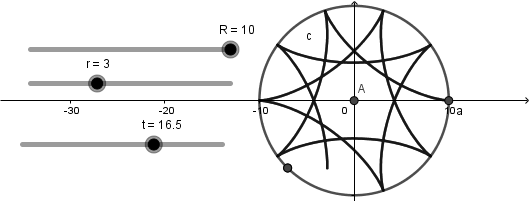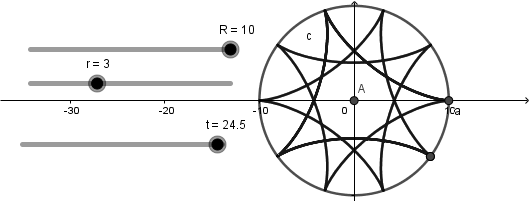
Al introducir las ecuaciones paramétricas se nos crearan dos deslizadores para "r" y "R" que no están definidas y por nuestra parte crearemos un deslizador "t", ademas se mostraran las gráficas correspondientes:

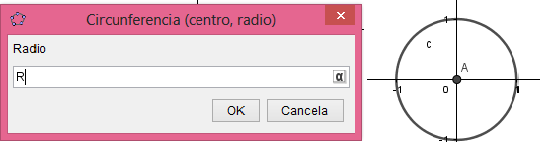
Luego de esto procederemos a crear la circunferencia directriz haciendo uso de la herramienta "centro , radio", y seleccionaremos como centro de la circunferencia el origen del eje cartesiano y pondremos como radio "R":
Luego de esto pasaremos a crear nuestra curva hipocicloide; haciendo uso del comando "curva", nos vamos a la barra de entrada escribimos curva y seleccionamos la siguiente configuracion:

En la primera casilla de
Expresión colocaremos
f(v)
en la segunda casilla
g(v)
como
parametro escribiremos
v
como
valor inicial colocaremos
0
y como
valor final t:
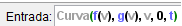
El resultado de hacer esto es una curva hipocicloide que se va creando a medida que avanza el deslizador "t":
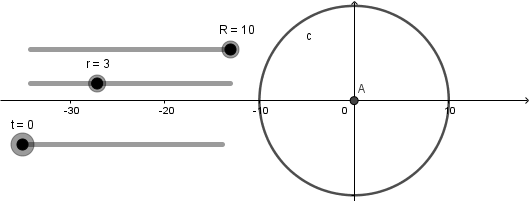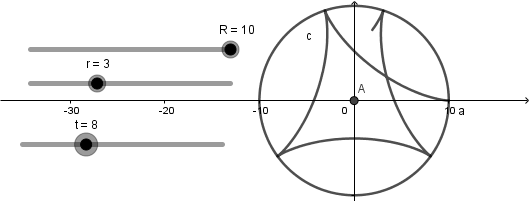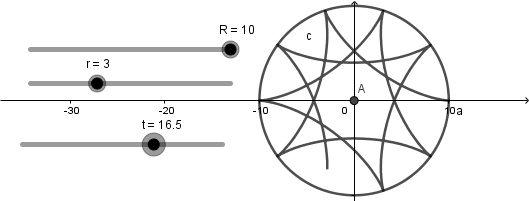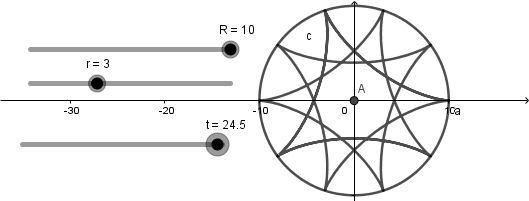
Luego de haber hecho todo esto debemos crear la circunferencia generatriz; para empezar crearemos un punto con definición (R,0) al cual le aplicaremos la herramienta rotación seleccionando como centro de rotación el centro de la circunferencia directriz y como angulo escribiremos "t" :
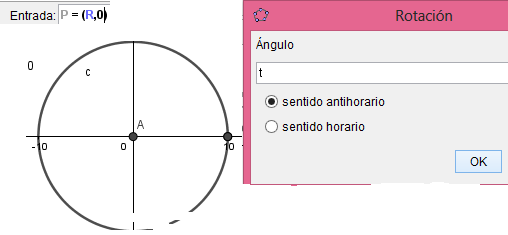
Lo cual nos da como resultado un punto que rota sobre la circunferencia directriz sincronizado con la curva hipocicloide, este punto nos servirá como base para la circunferencia generatriz:
Luego de haber hecho todo lo anterior haremos uso nuevamente de la herramienta centro, radio seleccionando como centro el punto móvil y colocando como radio "r" deslizador que corresponde según las ecuaciones paramétricas al radio de la circunferencia generatriz.
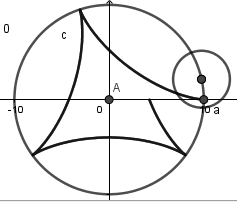
Esta circunferencia se moverá conforme avance el deslizador "t":
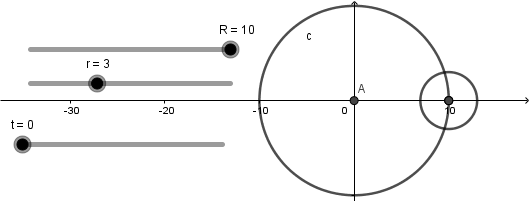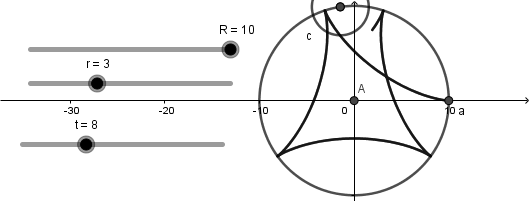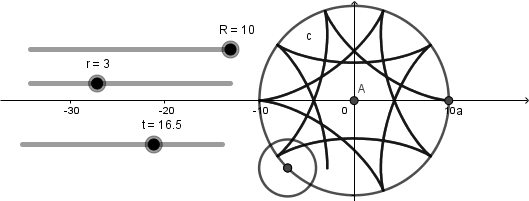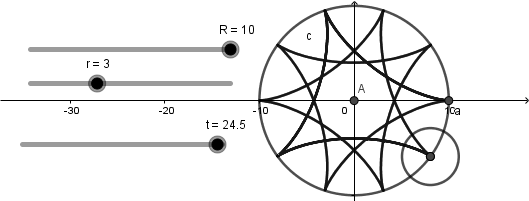
Sin embargo, como verán esta circunferencia no es la circunferencia generatriz ya que la generatriz debe estar dentro de la circunferencia directriz y esta circunferencia que hemos creado no cumple con esta característica pero nos ayudara a la creación de ella.
Primero crearemos una recta que pase por el centro de la circunferencia antes creada y el centro de la circunferencia directriz:
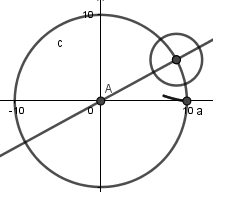
Luego de esto crearemos un punto en la intercepción interna de la circunferencia y la recta, este punto sera el centro de la circunferencia generatriz:
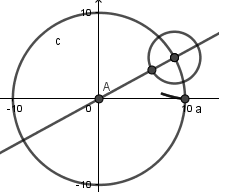
Hecho lo anterior procederemos a crear la circunferencia generatriz como tal; haciendo uso de la herramienta centro, radio crearemos una circunferencia con centro en el punto antes creado y radio "r":
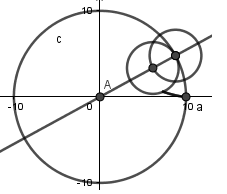
Como vemos esta circunferencia si esta dentro de la circunferencia directriz y al poner en marcha el deslizador "t" ocurre lo siguiente:
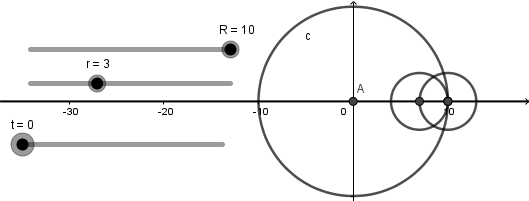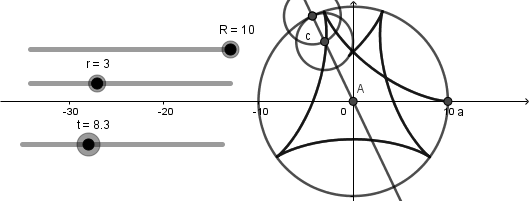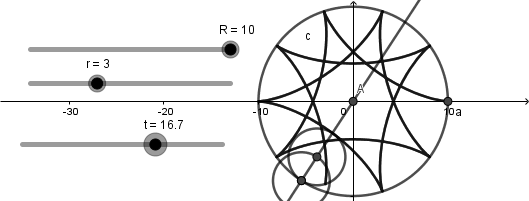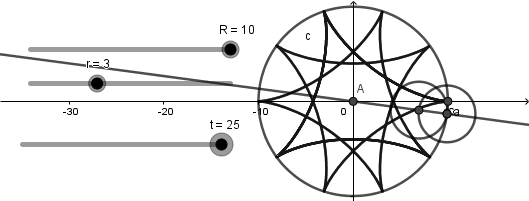
Llegado a este punto podemos decir que tenemos el 90% de nuestra simulación hecha, podemos ver una circunferencia rodando dentro de otra y una curva generándose, sin embargo, hace falta crear el punto sobre la circunferencia generatriz que describe la curva. Para esto nos iremos a la
barra de entrada y escribiremos:
La letra que corresponde a la curva seguido entre paréntesis "t"
:
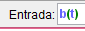
En mi caso la letra que se le asigno a mi curva fue "b", para ver que letra fue asignada solo deben dar click derecho sobre la curva, una vez hecho esto se creara un punto en el extremo de la curva sobre la circunferencia generatriz:
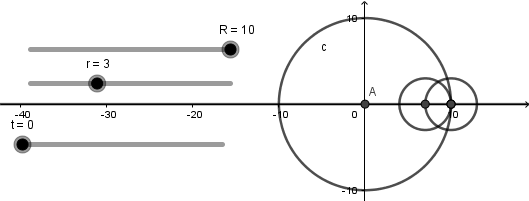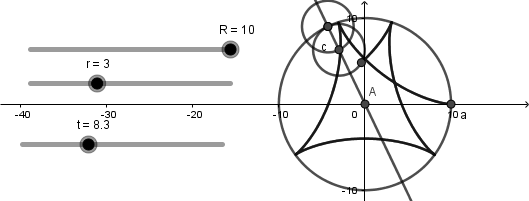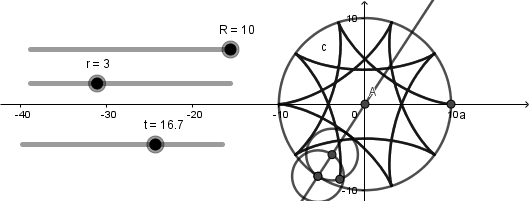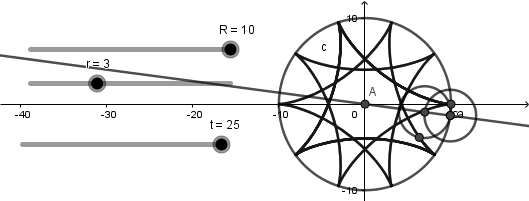
Como vemos el punto creado rota al rededor de la circunferencia generatriz al mismo tiempo que se crea la curva hipocicloide, llegados aquí ya tenemos nuestra simulación lista solo debemos ocultar los objetos no deseados, agregar colores y estilos de linea:
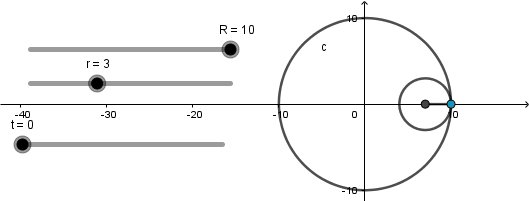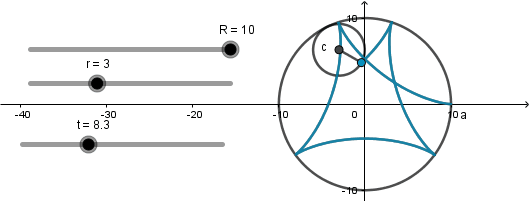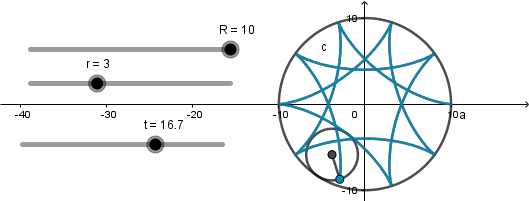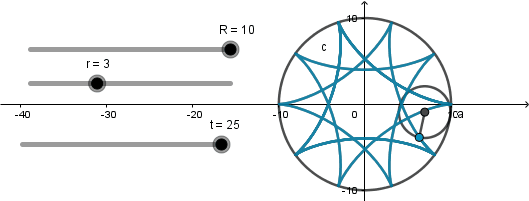
Terminada nuestra simulación solo nos queda jugar con los radios de las circunferencias mediante los deslizadores r y R , recordando que el radio de la circunferencia generatriz siempre debe ser menor que el de la circunferencia directriz.
Ejemplos
Deltoide: 3 vertices.
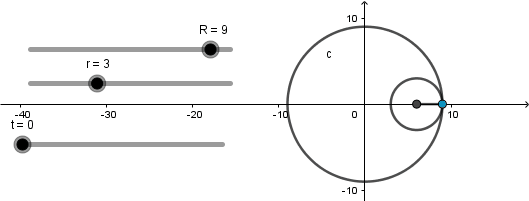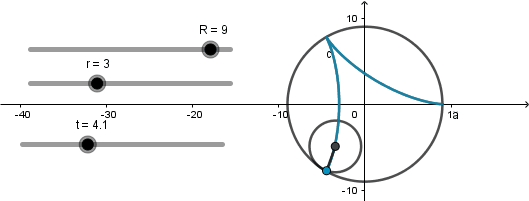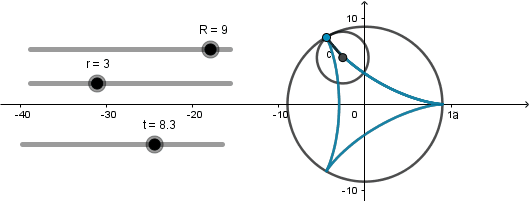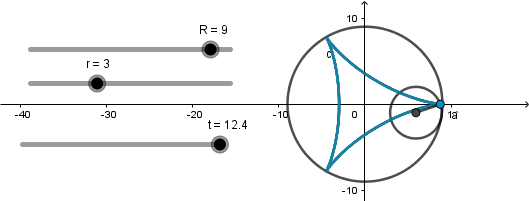
Se produce cuando el radio de la circunferencia directriz es tres veces el radio de la generatriz y en el caso especial cuando k = 4/3.
Astroide: 4 vertices.
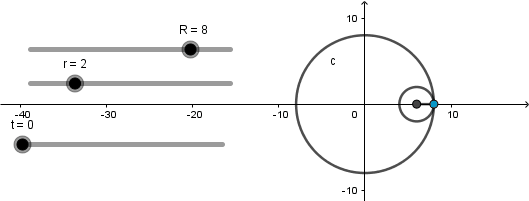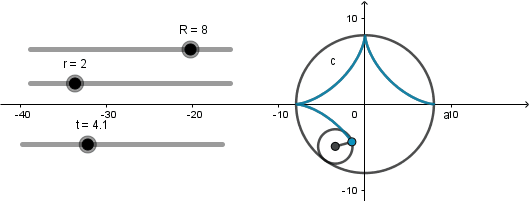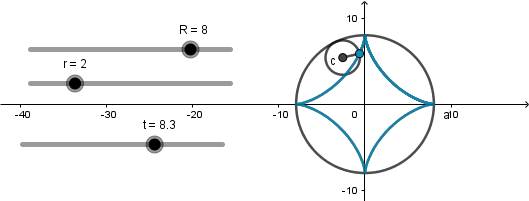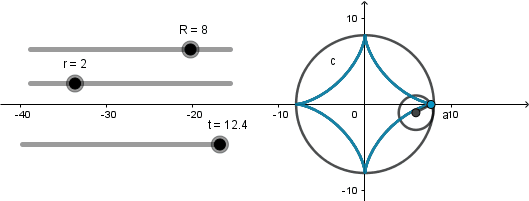
Se produce cuando el radio de la circunferencia directriz es cuatro veces el radio de la generatriz.
Estás dos curvas son quizás las más conocidas y representativas de curvas hipocicloide debido a sus interesantes características y propiedades, el número de vértices de la curva hipocicloide se debe al cociente "k" del radio de la circunferencia directriz y la generatriz. Además de esta hipocicloide tenemos dos tipos más al igual que con la cicloide y la epicicloide, la hipocicloide acortada y alarga; estás se dan cuando el punto que describe la curva está dentro de la circunferencia generatriz y fuera de esta respectivamente.
Hacer la simulación de estos dos tipos de hipocicloide es muy sencillo teniendo ya lista la simulación anterior, crearemos un deslizador "d" que representará la distancia a la que se encontrará el punto respecto al centro de la circunferencia generatriz, pondremos un
valor inicial de
r-1
y como
valor final r+1
Luego de creado el deslizador nos iremos a las ecuaciones paramétricas de la hipocicloide y modificaremos el segundo término cambiando
r
por
d
este valor corresponde a la distancia a la que se encuentra el punto que describe la curva:
Para el eje x.
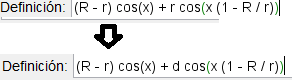
Para el eje y.
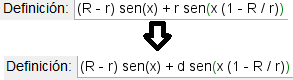
El resultado de esto es lo siguiente:
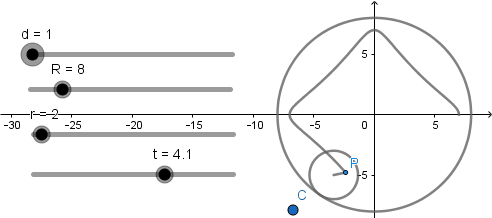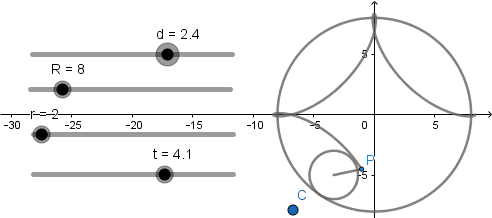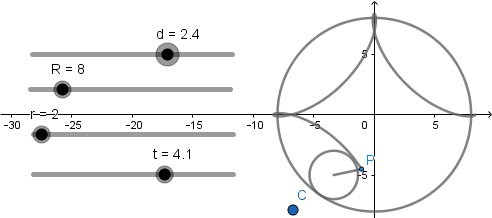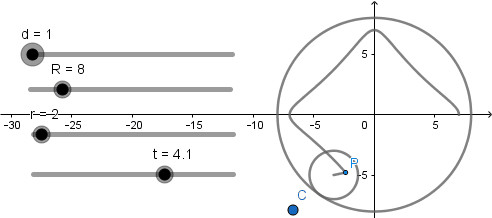
Hecho esto ya tenemos nuestras curvas epicicloide terminada en sus tres casos solo debemos mover el deslizador d para obtenerlas.
Ejemplos.
Los valores de la circunferencia generatriz y directriz corresponden a la generación de un astroide sin embargo, al tratarse de hipocicloide acortada y alargada obtenemos lo siguiente:
Hipocicloide acortada.
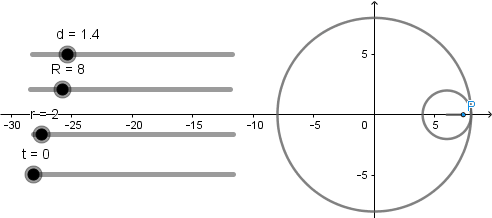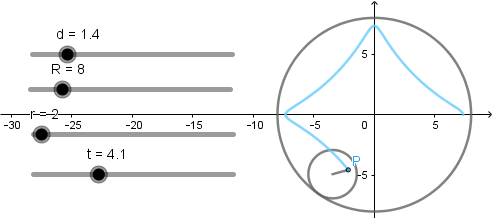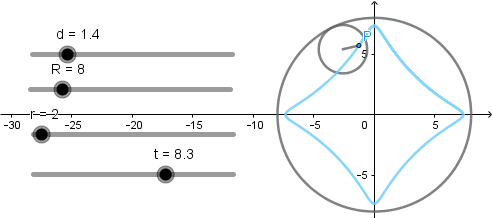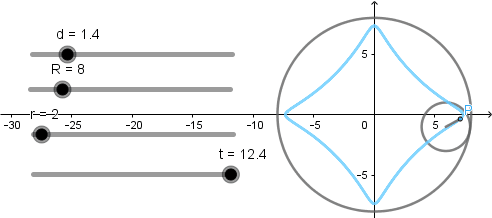
Hipocicloide alargada.
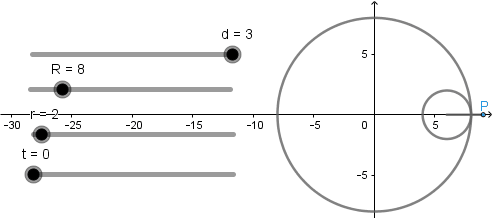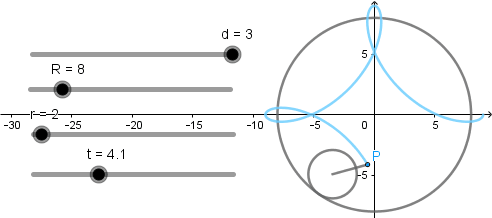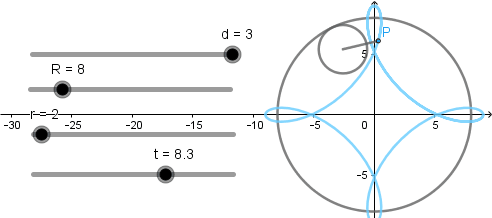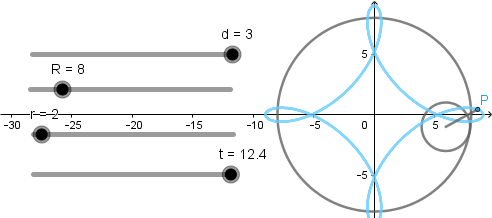
Podaria.
La podaria es el lugar geométrico formado por los puntos de corte entre cada tangente a una curva y la perpendicular a la tangente trazada respecto a un punto, la podaria de la hipocicloide es una rosa polar, esta curva es muy conocida normalmente presentada en las clases para llamar nuestra atención. Sabiendo el concepto de podaria solo debemos aplicarlo a nuestra simulación.
Para crear la tangente a la curva haremos uso de la herramienta tangente seleccionamos nuestra curva y el punto que describe la curva y se crea la tangente a esta:
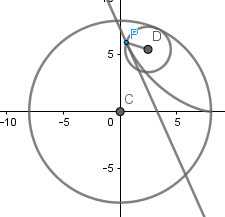
Luego de esto seleccionamos la herramienta de perpendicular y trazamos la perpendicular a la tangente seleccionando el centro de la circunferencia directriz y luego la tangente:
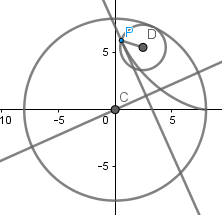
En el punto donde la perpendicular y la tangente se cortan crearemos un punto y activaremos su rastro, esto nos dará como resultado lo siguiente:
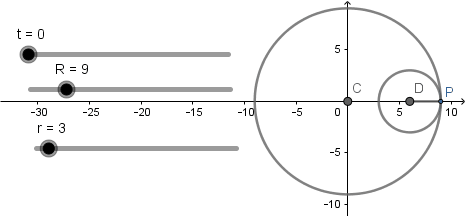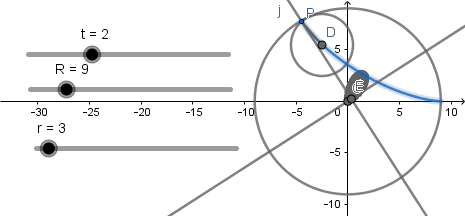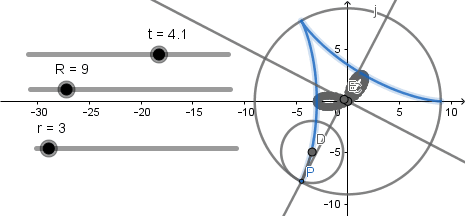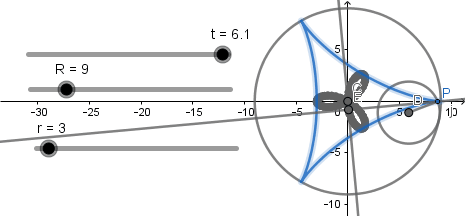
Como vemos y antes mencione la podaria es una rosa polar, en el caso del deltoide es una rosa polar de tres pétalos o trifolium.
El numero de pétalos de la rosa polar aumenta junto con el numero de vértices de la hipocicloide:
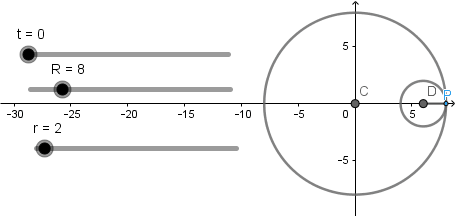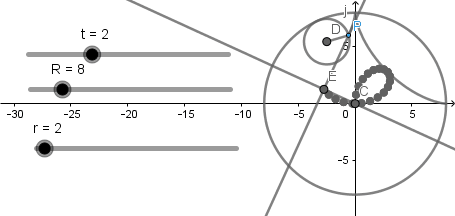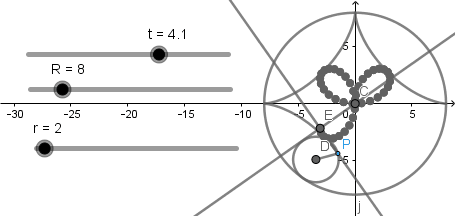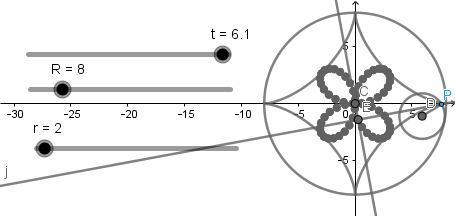
Astroide y su podaria.

Casos especiales de hipocicloide.
Lo interesante de la hipocicloide no solo se limita a bonitas curvas en forma de estrellas, podemos conseguir otras curvas como casos particulares de hipocicloide, un caso de esto es la generación de una elipse mediante hipocicloide en su versión acortada y alargada.
Elipse como hipocicloide acortada.
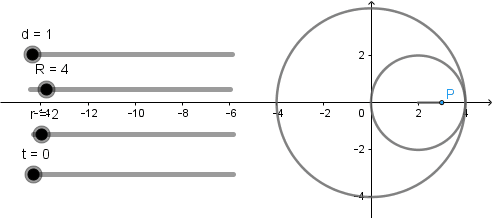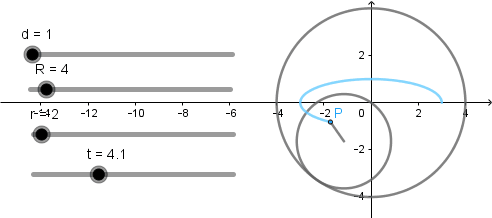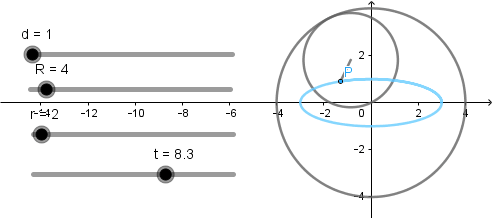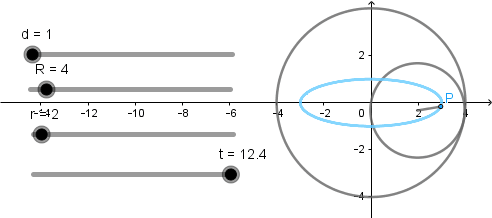
La elipse se produce cuando el radio de la circunferencia directriz es dos veces el radio de la circunferencia generatriz y el punto que describe la curva debe estar a una distancia de la mitad del radio de la circunferencia generatriz.
Elipse como hipocicloide alargada.
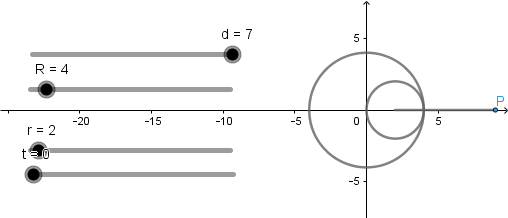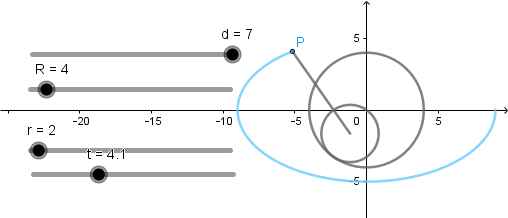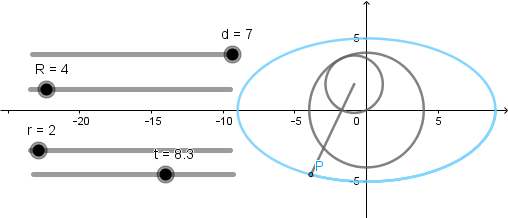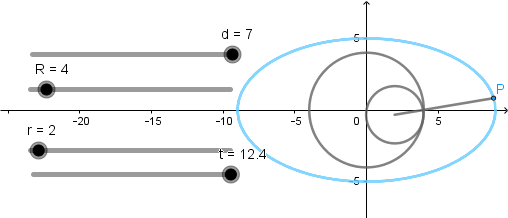
Como en el caso anterior el radio de la circunferencia directriz debe ser dos veces el radio de la circunferencia generatriz y el punto que describe la curva debe situarse a una distancia de siete veces el radio de la circunferencia generatriz.
Rosa Polar.
La hipocicloide y la rosa polar guardan una relación más y es que, podemos obtener una rosa polar como un caso especial de una hipocicloide alargada. Para esto establecemos 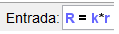 y
y 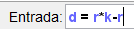 al hacer esto se eliminaran los deslizadores respectivos y ya tendremos nuestra hipocicloide como rosa polar, el numero de pétalos depende del valor del deslizador "k".
al hacer esto se eliminaran los deslizadores respectivos y ya tendremos nuestra hipocicloide como rosa polar, el numero de pétalos depende del valor del deslizador "k".
Ejemplos.
k = 3.
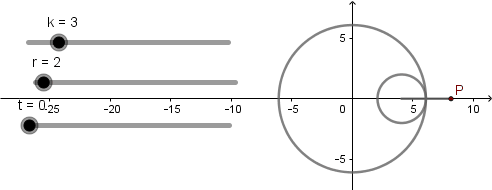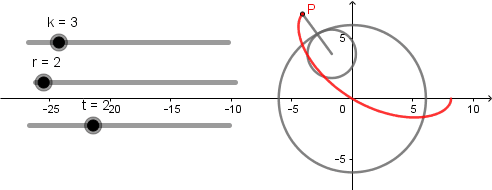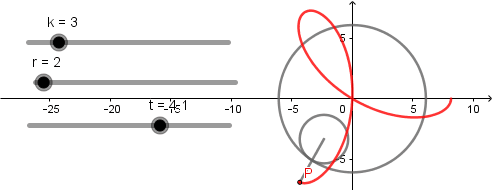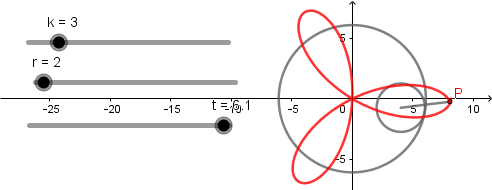
k = 4
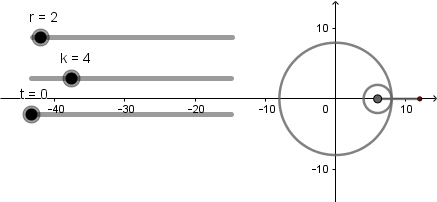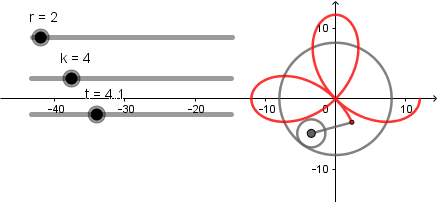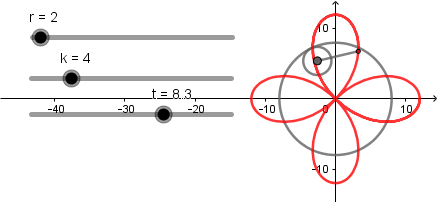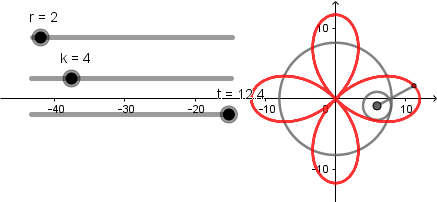
k = 9
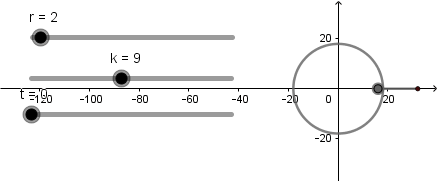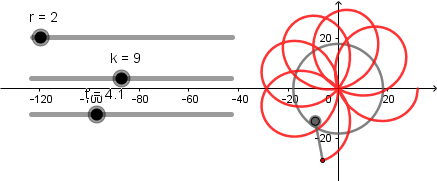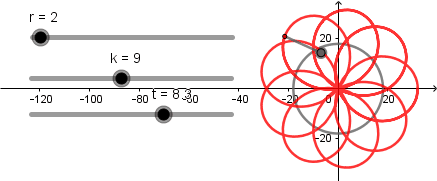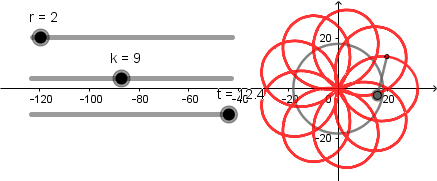
Y así tenemos listas las simulaciones para ser exportadas como animación GIF o cualquier otro formato que se desee, la curva hipocicloide es muy interesante tanto por las figuras que forma como por la relación que guarda con otras curvas si desean pueden interactuar con los applets de las animaciones desde la página de GeoGebra:
Solo deben mover los deslizadores para ir viendo las distintas formas que se crean al variar los radios, para los que están interesados en aprender a usar el software les dejo el archivo .ggb de las simulaciones creadas, les puede servir para guiarse aun más:
Si hacen uso de los applet me gustaría que me comentaran que les pareció :'D

Espero les haya gustado este post y empiecen a explorar este increíble software para crear por ustedes mismos sus animaciones.
Para leer contenido de calidad sobre ciencia los invito a visitar la etiqueta #stem-espanol.
Cualquier duda y sugerencia les agradecería que me la hicieran saber en los comentarios.
Todos las animaciones han sido hechas por mi usando el software GeoGebra Classic 5, las capturas de pantalla que he tomado pertenecen al mismo. 





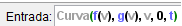














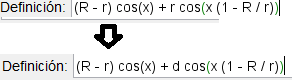
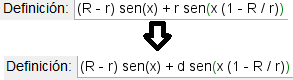





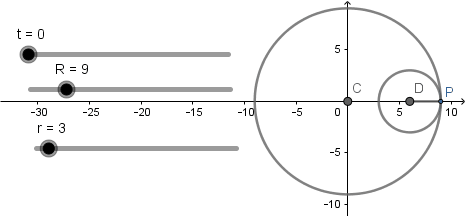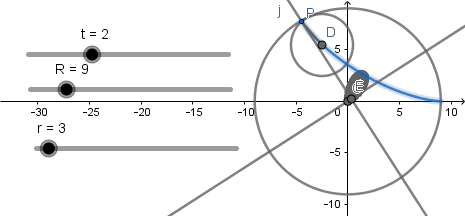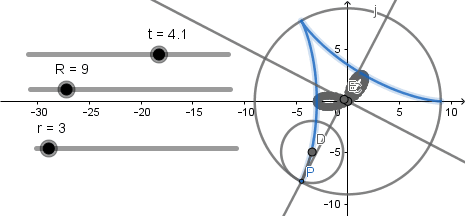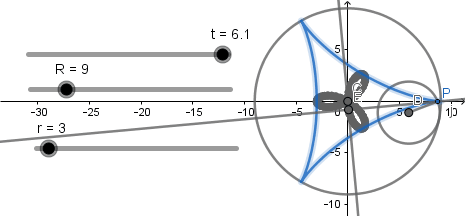
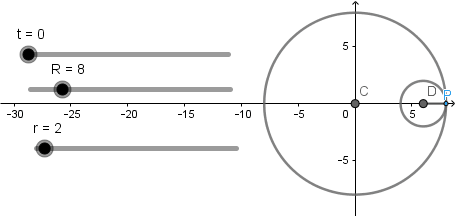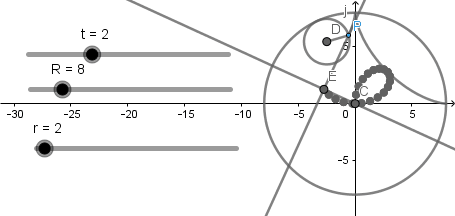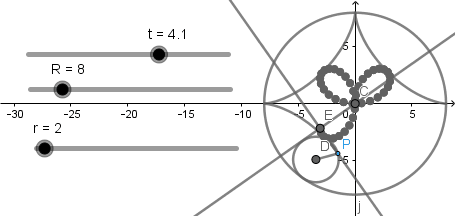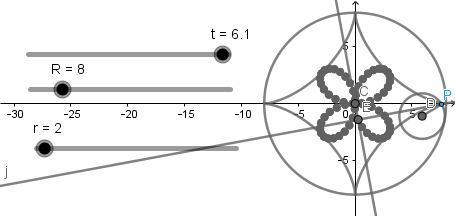


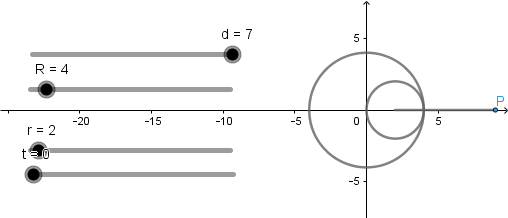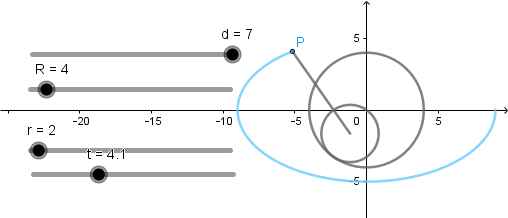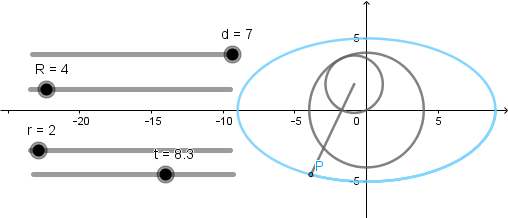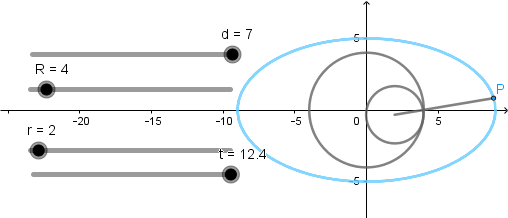
 y
y  al hacer esto se eliminaran los deslizadores respectivos y ya tendremos nuestra hipocicloide como rosa polar, el numero de pétalos depende del valor del deslizador "k".
al hacer esto se eliminaran los deslizadores respectivos y ya tendremos nuestra hipocicloide como rosa polar, el numero de pétalos depende del valor del deslizador "k". 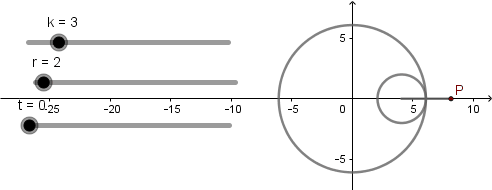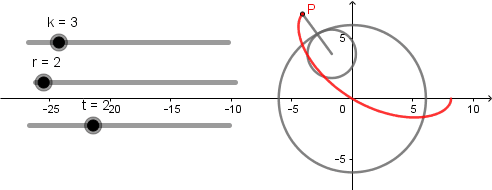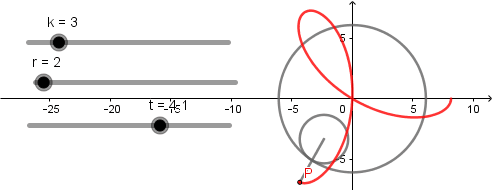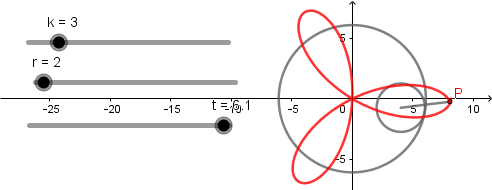
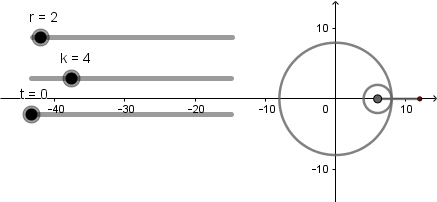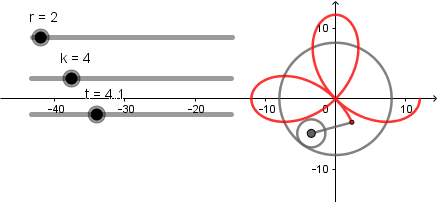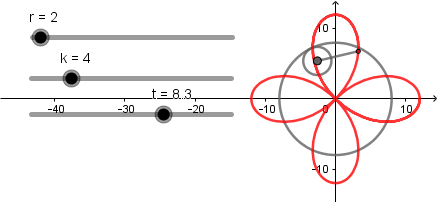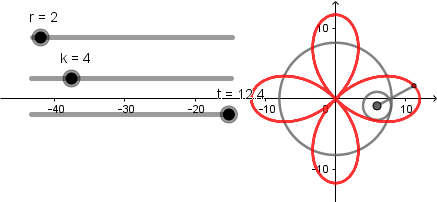
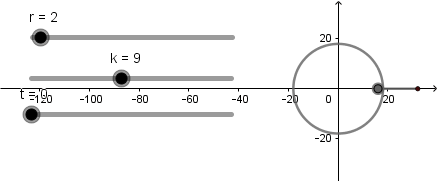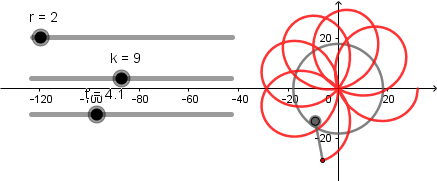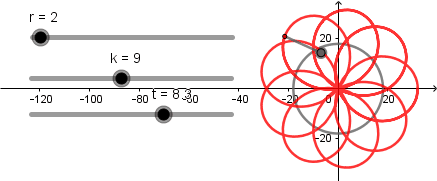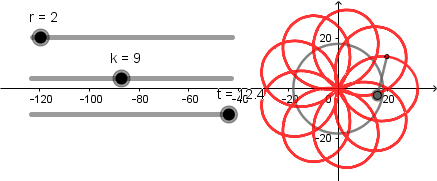

This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @luiscd8a!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Buen trabajo @luiscd8a, lo voy a reesteemear para revisarlo mejor. Si puedes saca otro post con simulaciones mas sencillas y cotidianas de la matemática y la física
Gracias @germanmontero, como que te gustaría ver?