Saludos estimados lectores espero se encuentren muy bien todos, luego de un largo receso vuelvo con mas física para todos; en esta oportunidad haremos una navegación por los principios y leyes que gobiernan la mecánica de fluidos en busca de comprender el comportamiento de estos y el entendimiento de algunos fenómenos que vivimos ya que estamos inmersos en ellos, los bebemos y respiramos estando presentes en cada día de nuestra vida.
¿Qué es un fluido?
Comúnmente al escuchar
fluido seguramente pensamos en algún liquido, ya sea agua, aceite o alguna bebida sin embargo no solo los líquidos son
fluidos, los gases también
fluyen por lo cual acogen este termino; decimos entonces que un
fluido es
cualquier sustancia que tenga la capacidad de fluir.
Una característica fundamental en el estudio de los fluidos es su densidad, sabemos que esta es la relación entre la masa y el volumen, es decir la cantidad de masa que podemos tener por unidad de volumen, en nuestro estudio consideraremos que la sustancia estudiada es homogénea lo cual se refiere a que su densidad es igual en todo punto, ademas de esto diremos que el fluido es incompresible y no hay fricción interna es decir despreciaremos su viscosidad.
Presión: Ley de Pascal.
Cuando un fluido se encuentra en reposo este ejerce una fuerza sobre cualquier superficie con la cual haga contacto, esta fuerza es perpendicular en todo punto a la superficie es decir, normal a la superficie.
Consideremos una pequeña superficie dA sumergida en un fluido.
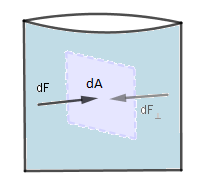
(Todas las imágenes han sido hechas por mi usando el software matemático GeoGebra Classic 5)
Como se observa el agua ejerce una fuerza de cada lado de la lamina, podemos definir la presión como la razón:
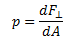
La presión es entonces la fuerza por unidad de área, si tenemos una superficie de área A y la fuerza ejercida en cada punto es la misma la presión viene dada por la fuerza neta aplicada sobre un lado de esta.
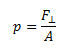
La presión y la fuerza son dos cantidades físicas distintas, su principal diferencia es que la presión es un escalar mientras la fuerza es un vector.
Quizás hayan escuchado que en la cima de una montaña la presion es menor, en este caso hablaríamos de la presión atmosférica que a mayor altura disminuye, de igual forman habrán escuchado y quizás notado que a mayor profundidad la presión aumenta, un ejemplo de esto sucede cuando al sumergirnos en una piscina o aguas profundas nuestros oídos se tapan; cuando el peso de un fluido es despreciable la presión en todo punto a través de el es la misma, en los ejemplos anteriores esto no es así, al sumergirnos mas y mas profundo en el agua el peso de esta "arriba" de nosotros no puede ser despreciado por lo cual es necesario definir una relación entre la presión en todo punto de un fluido en reposo y la altura.
Consideraremos un elemento de fluido homogéneo con superficies superior e inferior de área A y volumen dado por 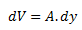 que, como todo el fluido se encuentra en reposo.
que, como todo el fluido se encuentra en reposo.
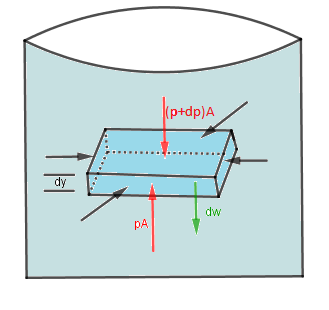
la masa del fluido es
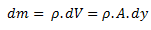
por lo cual su peso es
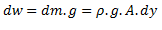
siendo
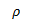
la densidad del fluido. El elemento de fluido se encuentra en reposo por lo cual todas las fuerzas debido a la presión están equilibradas incluyendo la debida al peso.
Al estar en reposo el elemento de fluido y al aplicar la segunda ley de Newton tenemos que:
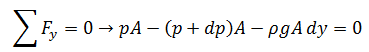
Al hacer las operaciones correspondientes y dividiendo entre el área obtenemos:
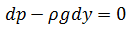
Reordenando:
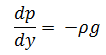
Esta ecuación nos dice que
a medida que la altura aumenta la presión disminuye
como se experimenta al subir una montaña o volar en un avión; por esta razón es necesario presurizar las cabinas.
Si reescribimos tenemos que:

Siendo 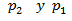 la presion a las alturas
la presion a las alturas 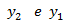 . La presión
. La presión 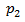 la situamos en la superficie del fluido, la diferencia
la situamos en la superficie del fluido, la diferencia 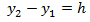
Lo anterior resulta en:
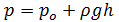
La ecuación anterior nos dice que la presión a una determinada profundidad es mayor que la presión en la superficie del fluido, de esta también se deduce que si la presión en la superficie aumenta esta de igual forma aumenta a cualquier profundidad en el fluido, esto es lo que se conoce como
Ley de Pascal
la cual nos dice que
la presión aplicada a un fluido en reposo se propaga de forme uniforme y sin perdida a través de todo este.
El funcionamiento de las prensas hidráulicas, frenos, elavadores y otros dispositivos hidráulicos se basan en esta Ley.
Se aplica una fuerza inicial sobre la superficie del fluido mediante un pistón:
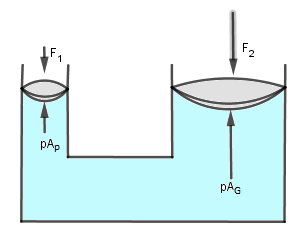
Donde la presión es:
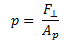
Esta presión se transmite por el fluido hasta llegar al segundo pistón de área mayor que el inicial, por lo cual tenemos que:
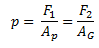
Para que esta igualdad se mantenga lo que ocurre es que, al ser mayor el área del segundo pistón la fuerza resultante debido a la presión sobre el aumenta considerablemente con respecto a la fuerza inicial, esto es aprovechado en diferentes sistemas hidráulicos ejemplo de esto son los gatos hidráulicos para los automóviles.

Flotabilidad: Principio de Arquímedes.
Todos algunas vez en nuestra vida hemos ido a una playa, un rio o simplemente a una piscina y entre todo ese disfrute y los juegos ocurren varias cosas que quizás pasan desapercibidas o simplemente son tan "comunes" que las ignoramos, por ejemplo, al jugar con una pelota dentro del agua podemos ver que al dejarla caer sobre la superficie de la piscina esta no se hunde o en otro caso si intentamos hundirla notamos que debemos hacer una fuerza considerable para mantenerla dentro del agua y al soltarla sale disparada, también y quizás lo mas significante poder levantar a una persona dentro del agua apenas haciendo un esfuerzo.
Si dejamos de ignorar estas cosas y empezamos a hacer un análisis sobre ellas llegamos a lo que hoy se conoce como
Principio de Arquímedes, principio enunciado por este célebre físico griego nos dice que:
un cuerpo sumergido parcial o totalmente dentro de un fluido en reposo recibe una fuerza de empuje hacia arriba igual al peso del fluido desplazado por este.
Consideramos una porción del fluido en reposo:
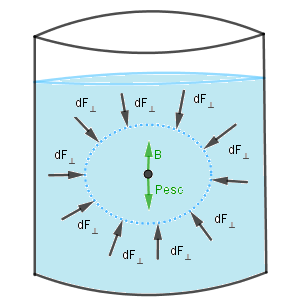
Al estar el fluido en reposo la suma de las componentes de fuerza que ejerce el fluido al rededor de este es cero como anteriormente habíamos visto, por lo tanto debe haber una fuerza resultante actuando hacia arriba igual al peso del fluido. Si ahora ingresamos un cuerpo solido de igual forma que la porción de fluido antes estudiada:
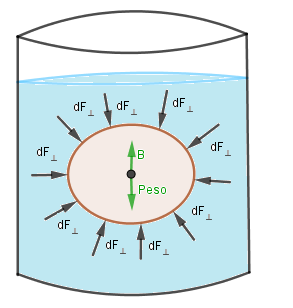
La presión ejercida por el fluido al rededor del cuerpo es exactamente igual en cada punto que en el caso de la porción de fluido, por lo tanto de igual forma la fuerza hacia arriba ejercida por el fluido es la misma de antes correspondiente al peso del fluido que el cuerpo desplaza, esta fuerza es la que se conoce como fuerza de flotación. Esta fuerza de flotación depende directamente de la densidad del fluido un fluido mas denso sugiere una fuerza de flotación mayor, esto explica el pequeño experimento que seguramente hayan visto en el cual se sumerge un huevo en un vaso con agua y este se hunde pero si agregamos cierta cantidad de sal al agua y volvemos a meter el huevo este flota, lo que ocurre es que al mezclar la sal en el agua aumentamos la densidad de esta lo que se traduce como vimos en una mayor fuerza de flotación.
Seguramente algunas vez se hayan preguntado como esos inmensos barcos logran flotar si una simple piedra se hunde en el agua, este principio nos da una respuesta; como ya sabemos la fuerza de flotación es igual al peso del fluido que se desplaza, estos inmensos barcos son construidos de tal forma que aunque la densidad del acero sea mayor que la del agua y por ende no flota en ella, con su gran superficie desplazan una cantidad de agua tal que el peso de esta es mayor que el peso total del barco, es decir una fuerza de flotación mayor que la fuerza debido al peso.
Para poner en evidencia lo anterior cortaremos dos laminas iguales de papel de aluminio:

(Todas las fotos han sido tomadas por mi con mi teléfono celular Siragon SP-5050)
Una la haremos una pequeña bolita y la otra la dejaremos igual:

Luego introducimos en un recipiente con agua:

Podremos observar que la bolita de papel de aluminio se hunde hasta el fondo del recipiente mientras la lamina se mantiene en la superficie.

La lamina de aluminio y la bolita pesan lo mismo, la única diferencia es su superficie y es esta la razón de que una flote y la otra no, pues la lamina al tener mayor superficie desplaza mayor cantidad de agua lo que se traduce como ya vimos en una mayor fuerza de flotación, esto es lo que ocurre con los barcos y sus grandes superficies de acero.

Flujo de fluidos: Ecuación de Bernoulli.
Habiendo conocido ya el comportamiento de los fluidos cuando se encuentran en reposo podemos pasar al estudio de estos en movimiento, el flujo de un fluido es laminar mayormente cuando este tiene una alta viscosidad y se mueve a bajas velocidades y turbulento cuando la viscosidad es baja y se mueve a altas velocidades.Un ejemplo de un flujo laminar es que el se da a través de una tubería, el humo del cigarrillo o el chorro de agua que sale de un grifo son un ejemplo de un flujo turbulento.
En nuestro estudio consideraremos que el flujo es estable, decimos que un flujo es estable cuando cada partícula del fluido que pasa por un punto sigue el mismo trayecto - linea de flujo - las lineas de flujo conforman un tubo de flujo con área A, en un flujo estable el fluido no puede cruzar las paredes del tubo por ende los diferentes tubos de flujo de un fluido no pueden mezclarse.
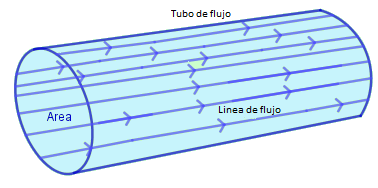
Al estar en movimiento un fluido su masa no cambia con lo que se puede obtener una relación considerando un tubo de flujo con areas A1 y A2 la velocidad del fluido al pasar por dichas áreas es 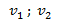 respectivamente
respectivamente
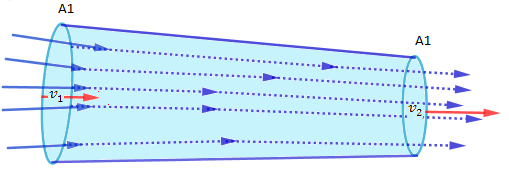
En un pequeño intervalo de tiempo dt el fluido pasa por el área A1 moviéndose una distancia:
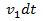
El volumen del fluido al atravesar el área A1 es:
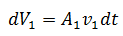
De igual forma el mismo intervalo de tiempo al cruzar el área A2 su volumen viene dado por:
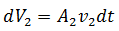
Al ser el fluido incompresible tiene la misma densidad en cada punto, su masa al fluir a través del área A1 es:
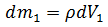
Al sustituir:
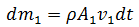
De igual forma la masa en A2 es:
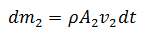
Sabemos que la masa no varia 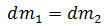 por lo tanto tenemos que:
por lo tanto tenemos que:
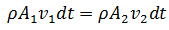
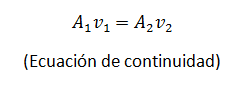
Llegamos a la tan conocida
ecuación de continuidad
la cual representa la
tasa de flujo de volumen vemos que sus unidades son de volumen por segundo es decir, la rapidez con que el volumen cruza una sección del tubo. Esta ecuación ademas nos muestra la conservación de la masa del fluido que es igual en todo punto sin importar el área del tubo de flujo o tubería por la cual fluye, si el área disminuye la velocidad del fluido aumenta y viceversa manteniéndose la tasa de flujo siempre constante.
Hemos visto como la rapidez de un fluido puede se variable a lo largo del recorrido que este haga y con esto la presión, todas estas variables se agrupan en una sola ecuación conocida como ecuación de Bernoulli para un flujo ideal.
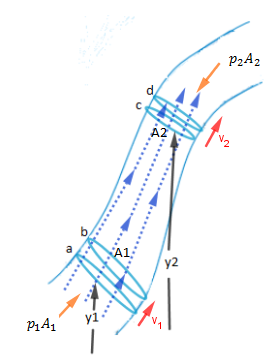
Consideraremos un elemento de fluido incompresible, en un tiempo dt se encuentra en
a y se mueve hasta
b una distancia
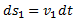
y de igual forma el fluido que esta en
c se mueve hasta
d una distancia
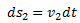
Por la ecuación de continuidad sabemos que el volumen de fluido a través de cualquier área es:
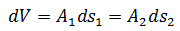
Ahora procedemos a calcular el trabajo efectuado sobre el elemento de fluido en el tiempo dt, sabemos que no hay viscosidad así que las fuerzas no conservativas que actúan sobre el elemento del fluido son solo las generadas por la presión del fluido al rededor de este, la fuerza sobre la seccion A1 es:
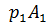
De igual forma la fuerza sobre la sección A2 es:
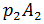
Por lo tanto el trabajo neto sobre el elemento de fluido es:
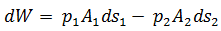
Lo que es igual a:
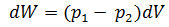
(1)
Este trabajo es causado por fuerzas no conservativas por lo tanto es igual al cambio de la energía mecánica total del elemento de fluido, recordemos que la energía mecánica total de un sistema viene dada por la suma de la energía cinética y potencial.
Sabemos que la energía cinética viene dada por:
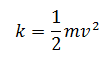
El fluido entre a y b
tiene una masa 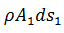 por lo tanto al sustituir en la expresión anterior obtenemos:
por lo tanto al sustituir en la expresión anterior obtenemos:
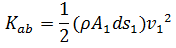
Al final del tiempo dt el fluido entre c y d
tiene una energía cinética:
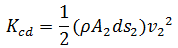
Por lo tanto el cambio neto de energía cinética es:
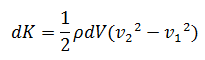
(2)
Por otra parte sabemos que la energía potencial viene dada por:
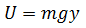
Por lo tanto entre las secciones a y b
la energía potencial es:
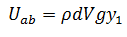
Y al final del tiempo dt en las secciones c y d
la energía potencial es:
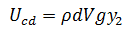
Por lo tanto el cambio neto de energía potencial es:
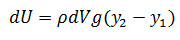
(3)
Finalmente solo debemos construir la ecuación de energía:
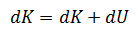
Sustituyendo (1), (2) y (3)
en la ecuacion anterior obtenemos:
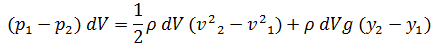
Simplificando:
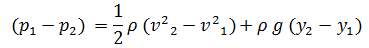
ECUACIÓN DE BERNOULLI.
A primera vista esta ecuación nos dice que el trabajo sobre un volumen de fluido realizado por el fluido que lo rodea es igual al cambio de la energía mecánica total que ocurre durante el flujo, por otra parte nos habla de los cambios de presión; el termino
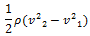
hace referencia a la diferencia de presión debido a los cambios de rapidez del fluido las zonas donde la rapidez del fluido es mayor presentan una presión menor respecto a una zona donde la rapidez del fluido es menor, el termino
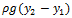
nos muestra la diferencia de presión debida al peso del fluido y la altura.

Material consultado:
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Young, H. D, & Freedman, R. A. FISICA UNIVERSITARIA, volume 1. Pearson Educación de México, S.A. de C.V., 2009.
Todas las imágenes han sido hechas por mi usando el software matemático GeoGebra Classic 5 y las fotografías han sido tomadas por mi.
Espero hayan disfrutado de este contenido y aprendido un poco sobre el comportamiento de los fluidos pudiendo así interpretar algunos fenómenos que nos rodean.
Si desean leer mas contenido sobre ciencia los invito a visitar la etiqueta #STEM-espanol

Imagen creada por @djredimi2

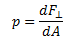
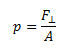
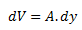 que, como todo el fluido se encuentra en reposo.
que, como todo el fluido se encuentra en reposo. 
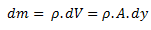 por lo cual su peso es
por lo cual su peso es 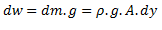 siendo
siendo 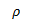 la densidad del fluido. El elemento de fluido se encuentra en reposo por lo cual todas las fuerzas debido a la presión están equilibradas incluyendo la debida al peso.
la densidad del fluido. El elemento de fluido se encuentra en reposo por lo cual todas las fuerzas debido a la presión están equilibradas incluyendo la debida al peso. 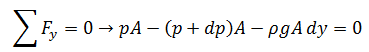
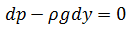
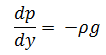

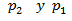 la presion a las alturas
la presion a las alturas 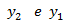 . La presión
. La presión 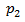 la situamos en la superficie del fluido, la diferencia
la situamos en la superficie del fluido, la diferencia 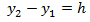
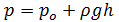

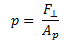
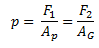









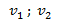 respectivamente
respectivamente 
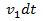
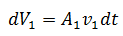
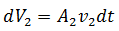
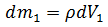
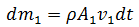
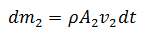
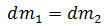 por lo tanto tenemos que:
por lo tanto tenemos que: 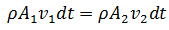
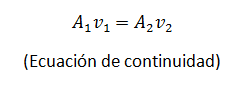

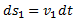 y de igual forma el fluido que esta en c se mueve hasta d una distancia
y de igual forma el fluido que esta en c se mueve hasta d una distancia 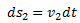
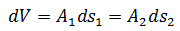
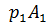
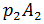
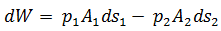
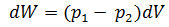
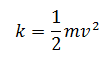
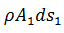 por lo tanto al sustituir en la expresión anterior obtenemos:
por lo tanto al sustituir en la expresión anterior obtenemos: 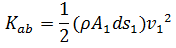
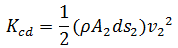
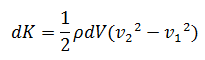
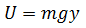
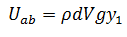
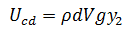
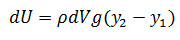
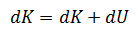
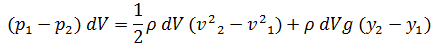
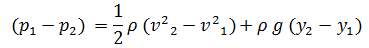
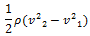 hace referencia a la diferencia de presión debido a los cambios de rapidez del fluido las zonas donde la rapidez del fluido es mayor presentan una presión menor respecto a una zona donde la rapidez del fluido es menor, el termino
hace referencia a la diferencia de presión debido a los cambios de rapidez del fluido las zonas donde la rapidez del fluido es mayor presentan una presión menor respecto a una zona donde la rapidez del fluido es menor, el termino 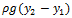 nos muestra la diferencia de presión debida al peso del fluido y la altura.
nos muestra la diferencia de presión debida al peso del fluido y la altura. 

This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @luiscd8a!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV