Espectroscopia de Reflectancia Difusa
Saludos comunidad #Steemit y #Stem-espanol, hoy quiero compartir con ustedes un poco sobre la espectroscopia de Reflectancia Difusa, es una técnica que use para caracterizar muestras de arcillas, predomina en materiales débilmente absorbentes de tipo coloides y ha ganado especial atención en los últimos años en la caracterización óptica de materiales sólidos, a continuación muestro el principio físico de este técnica.
Al incidir radiación electromagnética sobre una muestra la reflexión de la radiación puede ser de dos tipos: especular y difusa. Generalmente las medidas de reflectancia contienen ambos tipos de reflexión, la especular (superficial), brinda poca información sobre la composición de la muestra, mientras que en la reflexión difusa se basan las medidas cuantitativas y corresponde a aquella que es absorbida temporalmente por la muestra antes de ser re-emitida. La energía total reflejada equivale a la suma de la reflexión especular y difusa. En los últimos años esta técnica ha ganado un especial interés en el estudio de muestras de polvo fino de tipo coloide, es una técnica no destructiva y no requiere de una preparación previa de la muestra en estudio. .
Para comprender mucho mejor el principio físico considere la figura 1 donde se muestra los posibles tipos de reflexión de la radiación sobre un material, el cual puede ser especular, irregular y difusa.
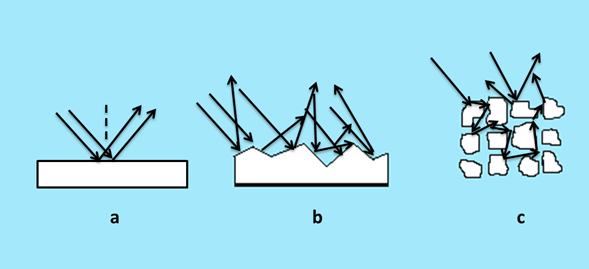
Las ecuaciones de Fresnel gobiernan la reflexión especular (figura 1a), donde la relación de la intensidad reflejada y la intensidad total incidente dependen de los índices de difracción del aire y de la muestra. Si se considera el caso donde la superficie es irregular (figura 1b) se observa que la muestra está compuesta por pequeñas superficie orientadas en diversas direcciones y en todos los ángulos posibles, la luz se refleja según Fresnel en cada pequeña interface pero la reflexión global corresponde a la reflexión en todas las direcciones. Finalmente al considerar el último caso (figura 1c) se observa que la muestra está compuesta por diversas capas de partículas, la radiación incidente es capaz de traspasar la primera capa y propagarse a través de capas más profundas mediante refacciones y dispersiones.
De igual manera, en la figura 2 se observan los fenómenos de reflexión especular y difusa sobre un material de manera más clara, el rayo incidente 1 llega a la superficie de los cristales pero no tiene interacciona con la muestra, produciendo un rayo de reflexión especular, mientras que el caso del rayo indicen 2 se produce la absorción debido al ángulo de incidencia, en este caso el rayo interactúa con la muestra y se producen sucesivas refracciones y difracciones, al ocurrir esto el rayo es refractado y reflectado en varias direcciones antes de ser re-emitido por la muestra, estos rayos interaccionan con la muestra generando información como naturaleza y composición lo cual corresponde a la reflectancia difusa.
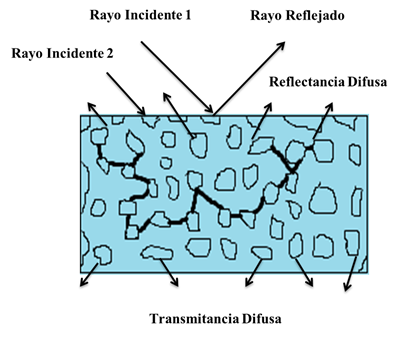
Esta técnica ha ganado especial interés en los últimos años debido a la capacidad de caracterizar partículas dispersivas, muestras de tipo coloide en los cuales el camino óptico que recorre la luz es difícil de establecer debido a los fenómenos de absorción y dispersión mencionados anteriormente. Se han desarrollados varias teorías con el fin de entender el comportamiento de la luz en este tipo de sistemas dispersivos, una de las más ampliamente usadas y aceptadas en los últimos tiempos corresponde a un modelo basado en una serie de resoluciones de ecuación diferenciales conocido como el modelo de Kubelka-Munk, el cual describe la disminución de la intensidad de la radiación debido a la dispersión y absorción.
Si se considera que el espesor de la capa de una muestra solida es infinito o bien un sólido completamente opaco, se cumple que:
Donde F(R∞) es una función de remisión por lo que FKM es conocida como la función de remisión de Kubelka-Munk, R∞ es la reflectancia de la capa infinitamente gruesa y k y s son las constante de absorción y dispersión, respectivamente. Para muestras ópticamente gruesas esta función de la reflectancia difusa tiene una dependencia lineal con el coeficiente de absorción del material. Es posible calcular la función Kubelka-Munk a partir de los datos de absorción medidos por reflectancia difusa y permite determinar el valor de la banda prohibida o Band Gap de una muestra, mediante la ecuación 3 considerando que la dispersión es homogénea se cumple lo siguiente:
La representación gráfica de (𝑅∞) versus la energía del fotón (ℎ𝑣) permite obtener el valor del ancho de banda prohibida, mediante la comparación de la ecuación 3 con la ecuación de la linea recta, al realizar una regresión lineal de la parte más recta de la curva obtenida y extrapolando la recta asumiendo que (𝑅∞) = 0 se encuentra la intersección con el eje de las abscisas (ℎ𝑣), que corresponde al valor del ancho de banda prohibida (𝐸𝑔).
Mediante el modelo de Kubelka-Munck se determinó la brecha energética de arcillas naturales venezolanas, para lo cual se usó un espectrómetro UV-Vis-NIR U-3101 PC Shimadzu, empleando un intervalo de longitud de onda de 200-2500 nm, con accesorio de reflectancia difusa MPC-3100 Shimadzu, equipado con una esfera integradora, empleando BaSO4 como referencia (100% reflectancia). Estas mediciones se realizaron a temperatura ambiente, usando pastillas del material arcilloso finamente triturado.
La figura 3 muestra un espectrograma tipico de reflectancia difusa en el rango energético de UV-Visible correspondiente a la arcilla natural proveniente de Tinaquillo.
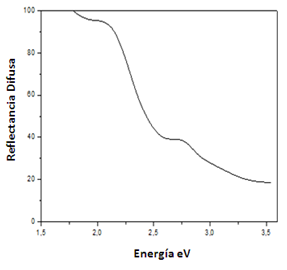
En el espectrograma de la figura 3, se observa una reducción considerable de la reflexión en la región cercana a 2,5 eV. Esta disminución de la reflexión se asocia a la absorción y dispersión de las partículas sólidas de la arcilla.
A partir del espectro de reflectancia difusa no es posible evaluar el coeficiete de absorción asociado al sistema en estudio. En medios dispersivos el camino óptico recorrido por la luz es difícil de establecer, ya que la disminución de la radiación se debe a la absorción y dispersión. Para determinar el coeficiente de absorción se requiere de un tratamiento matemático basado en la teoría de Kubelka-Munk, a través del cual se obtiene un espectrograma de absorción convertido a partir del cual es posible determinar la brecha energética del material estudiado (ver ecuación 1 y 3). El espectro de Kubelka-Munk correspondiente a la arcilla natural Tinaquillo se muestra en la figura 4.
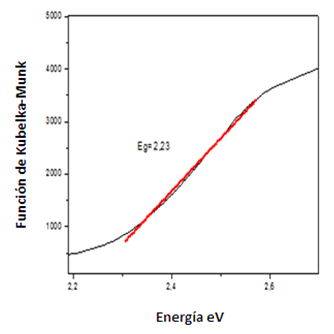
Como se observa en la Figura 4, para la arcilla natual de Tinaquillo, la función de Kubelka-Munk presenta una tendencia lineal con el aumento de la energía. La regresión lineal de la región más recta de esta curva y la extrapolación al eje de las abscisas determina el valor del ancho de banda prohibida o brecha energética. Para la arcilla Tinaquillo el valor de la brecha energética (Eg) fue de 2,23 eV, es decir, ocurre una transición electrónica en el rango visible del espectro electromagnético.
Mediante esta técnica es estudiaron varias arcillas naturales venezolanas, los resultados obtenidos mediante la aplicación del modelo de Kubelka-Munk, sugieren que los materiales estudiados poseen una estructura de bandas similar a la estructura de bandas de un material semiconductor. La brecha energética de los materiales estudiados oscila entre 2,20-2,37 eV. Estos valores son comparables a los de un grupo de semiconductores comunes y ampliamente utilizados (Tabla 1) y sugieren que los materiales estudiados pueden tener propiedades semiconductoras.
| Semiconductor | Eg (eV) |
|---|---|
| Sulfuro de Cadmio (CdS) | 2,24 |
| Fosfuro de galio (III) (GaP) | 2,24 |
| Sulfuro de Cadmio (CdS) | 2,25 |
| Óxido de cobre (II) Cu2O | 2,17 |
Entre las conclusiones más importantes de este trabajo se destaca que mediante la aplicación del modelo de Kubelka-Munk basado en medidas de reflectancia difusa se determinaron las transiciones electrónicas de minerales presentes en la naturaleza de manera abundante en el rango visible del espectro, que según este modelo estas transiciones corresponde a la brecha energética de estos materiales. Los valores de Eg determinados son similares a la de semiconductores conocidos de amplio rango de aplicaciones.
Referencias:
- Rojas I., MoraC., Herrera H., 2007, “Bandas de energía y consecuencias”, Latin-American Journal of Physics Education, 1, 89-94.
- Cirpan, A., Ding, L., &Karasz, F. E. (2005). Optical and electroluminescent properties of polyfluorene copolymers and their blends. Polymer, 46(3), 811-817.
- Tipler A., Mosca G., 2005, “Física para la ciencia y la tecnología” Editorial Reverte, vol 2, 1147.
- Burbano S., Gracia C., 2003, “Física General”. Editorial Tébar, p 453.
- Portis A., Young H., 1974, Electrónica de Semiconductores, Editorial Reverte, edición 2, vol. 12, 2-3
- Callister W., 2007, “Ciencia e Ingeniería de los materiales”, Editorial Reverte, Barcelona España, 404.
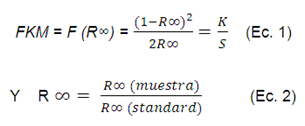
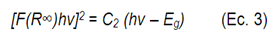
Saludos estimada @rossyholg. Es interesante el enfoque que le dan los químicos a estudios ópticos en arcillas. Mi pregunta siempre ha sido:
Por que asocian a las arcillas con los semiconductores?
Pues, el término "Semiconductor" esta íntimamente asociado a las propiedades eléctricas y no a los fenómenos ópticos! Pueden ser cristales ¡de hecho lo son! pero son las arcillas semiconductores?
Gracias de antemano estimada.
Saludos rossyholg, buen aporte sobre espectroscopia, felicitaciones comenzaré a seguirte.
I strive not to be a man of success, but rather to be a man of value.