Angulo sólido subtendido por un disco con respecto a un punto que se encuentra dentro y fuera de su eje de simetría.
Aquí estoy nuevamente mis estimados y atentos Steemians-Lectores, saludos para todos. Continuando con mi disertación acerca del Angulo Sólido, esta vez les muestro la forma de calcular el Angulo sólido subtendido por un disco con respecto a un punto que se encuentra dentro y fuera de su eje de simetría. Todo esto lo hago con la finalidad, como es mi costumbre, de hacer más fácil de entender todos los procedimientos involucrados.
DEBO DESTACAR, MIS ESTIMADOS AMIGOS STEEMIANS-LECTORES, QUE EL ESTUDIO DEL ANGULO SOLIDO ES MUY IMPORTANTE EN VARIOS CAMPOS DE LA CIENCIA, ESPECIALMENTE EN EL CAMPO DE LA FISICA MEDICA CUANDO SE TRATA DE LA DETECCION Y DOSIFICACION DE RADIACION. EN ESTE CAMPO EL ANGULO SOLIDO TIENE DIRECTA RELACION CON LA EFICIENCIA GEOMETRICA DE LOS DETECTORES DE RADIACION Y EN LA APLICACION DE DOSIS DE RADIACION EN EL CUERPO HUMANO. POR ESTA RAZON, EN LA ACTUALIDAD, SE SIGUE DEDICANDO MUCHO TIEMPO Y ESFUERZO EN SU ESTUDIO EN ESTA AREA Y, POR LO MISMO, YO HE INTENTADO DESARROLLAR (CON TODA ESTA SERIE DE POSTS) DE FORMA CLARA Y SENCILLA LA TEORIA RELACIONADA, LA CUAL SERIA DE GRAN APOYO PARA LOS STEEMIANS QUE HAGAN CARRERA EN EL AREA ANTES MENCIONADA. MATERIAL SOBRE EL ANGULO SOLIDO ES ESCASO. |
|---|
Para tener una excelente abordaje del material presentado en este post, les recomiendo leer previamente mis posts:
- EL ANGULO SOLIDO - PARTE 1 - CONOCIMIENTOS BASICOS.
- EL ANGULO SOLIDO - PARTE 2 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 3 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 4 - CONOCIMIENTOS BASICOS (CONTINUACION).
- EL ANGULO SOLIDO - PARTE 5 - DEFINICION DE ANGULO SOLIDO.
- EL ANGULO SOLIDO - PARTE 6 - EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO.
- EL ANGULO SOLIDO - PARTE 7 - PROPIEDADES DEL ANGULO SOLIDO.
- ANGULO SOLIDO SUBTENDIDO POR UNA DE LAS CARAS DE UN CUBO CON RESPECTO A UN PUNTO SITUADO EN EL CENTRO DEL MISMO
- ANGULO SOLIDO SUBTENDIDO POR UNA PLACA RECTANGULAR CON RESPECTO A UN PUNTO SITUADO DIRECTAMENTE SOBRE UNO DE SUS VERTICES.
- ANGULO SOLIDO SUBTENDIDO POR UNA PLACA RECTANGULAR CON RESPECTO A UN PUNTO SITUADO EN SU EJE DE SIMETRIA.
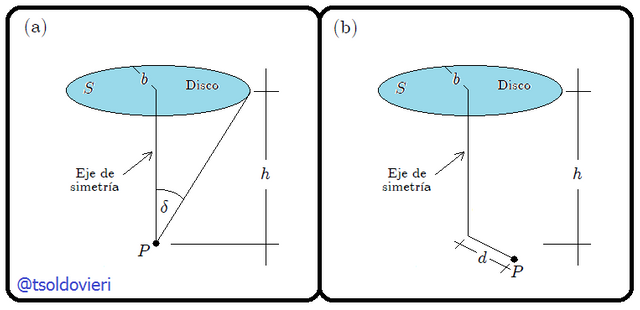
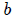 que se encuentra a una distancia
que se encuentra a una distancia 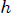 de un punto
de un punto 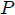 ubicado sobre su eje de simetría. (b) Disco de radio
ubicado sobre su eje de simetría. (b) Disco de radio 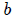 que se encuentra a una distancia
que se encuentra a una distancia 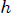 de un punto
de un punto 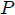 ubicado a una distancia
ubicado a una distancia 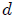 de su eje de simetría, en un plano paralelo al disco.
de su eje de simetría, en un plano paralelo al disco.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
Atentos amigos Steemians-Lectores deseamos, en esta oportunidad, calcular el Angulo Sólido 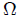 subtendido por un disco de radio
subtendido por un disco de radio 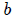 con respecto a un punto
con respecto a un punto 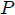 que se encuentra a una distancia
que se encuentra a una distancia 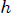 del mismo, dentro y fuera de su eje de simetría. Lo anterior se los muestro en la figura 1(a) y 1(b).
del mismo, dentro y fuera de su eje de simetría. Lo anterior se los muestro en la figura 1(a) y 1(b).
(a) - Con respecto a un punto que se encuentra dentro de su eje de simetría:
(a.1) Usando coordenadas cilíndricas:
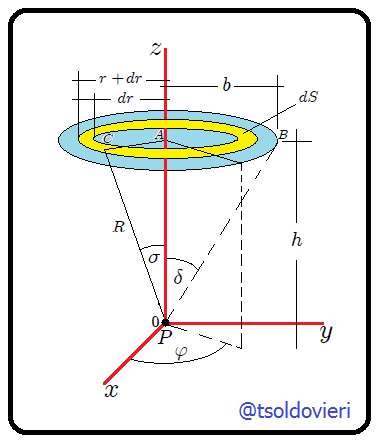
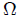 subtendido por el disco con respecto a
subtendido por el disco con respecto a 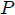 usando coordenadas cilíndricas.
usando coordenadas cilíndricas.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
Con la finalidad de usar 6 en el post EL ANGULO SOLIDO - PARTE 6 - EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO para calcular el Angulo Sólido 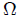 , se recubrirá toda
, se recubrirá toda 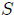 mediante una serie de coronas circulares concéntricas como les presento en la figura 2. El radio interno de cada una de estas superficies es
mediante una serie de coronas circulares concéntricas como les presento en la figura 2. El radio interno de cada una de estas superficies es 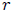 y el radio externo es
y el radio externo es 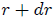 , de manera que la superficie de cada corona circular viene dada por,
, de manera que la superficie de cada corona circular viene dada por,
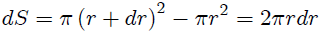
donde he despreciado el término de segundo orden de 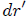 ya que éste es infinitesimalmente pequeño. Atentos Steemians-Lectores, es fácil determinar a partir del triángulo
ya que éste es infinitesimalmente pequeño. Atentos Steemians-Lectores, es fácil determinar a partir del triángulo 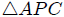 que cada punto sobre la corona circular está a una distancia de
que cada punto sobre la corona circular está a una distancia de 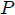 dada por,
dada por,
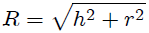
y además,
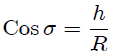
entonces, a partir de la definición 6 en el post EL ANGULO SOLIDO - PARTE 6 - EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO el ángulo sólido buscado 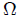 vendrá dado por,
vendrá dado por,
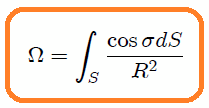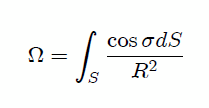
Ahora bien, al sustituir los resultados (2) y (3) en (4) nos resulta,
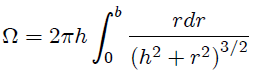
que al ser integrada nos resulta finalmente en,
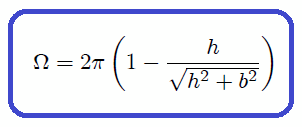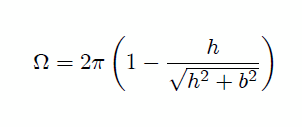
siendo este resultado el Angulo Sólido buscado.
(a.2) Usando coordenadas esféricas:
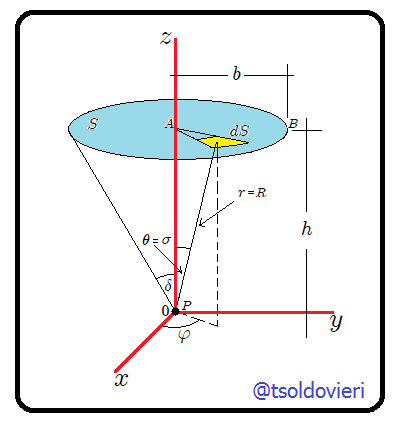
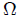 subtendido por el disco con respecto a
subtendido por el disco con respecto a 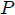 , usando coordenadas esféricas.
, usando coordenadas esféricas.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
Si empleamos coordenadas esféricas (observen la figura 3), el diferencial de ángulo sólido vendrá dado a partir de (4) en ANGULO SOLIDO SUBTENDIDO POR UNA PLACA RECTANGULAR CON RESPECTO A UN PUNTO SITUADO EN SU EJE DE SIMETRIA mediante,
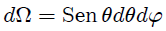
entonces,
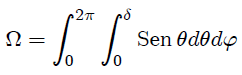
donde 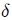 es el valor que toma
es el valor que toma 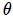 en el borde del disco, es decir, es el semiángulo subtendido por el disco con respecto a
en el borde del disco, es decir, es el semiángulo subtendido por el disco con respecto a 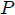 . Al integrar nos resulta,
. Al integrar nos resulta,
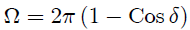
Ahora como,
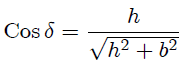
entonces de (9) nos resulta,
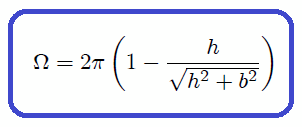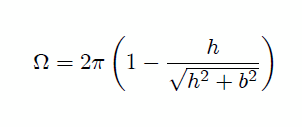
siendo idéntico al resultado (6), como era de esperarse.
(b) - Con respecto a un punto que se encuentra fuera de su eje de simetría:
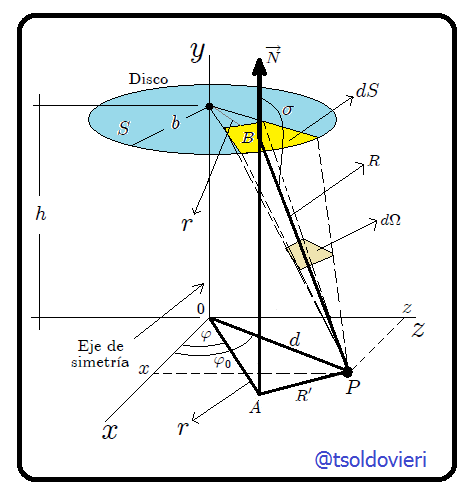
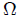 para un disco de superficie
para un disco de superficie 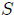 y de radio
y de radio 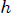 que se encuentra a una distancia
que se encuentra a una distancia 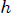 de un punto
de un punto 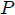 ubicado fuera de su eje de simetría.
ubicado fuera de su eje de simetría.(Figura realizada por mi persona, @tsoldovieri, usando la aplicación Paint)
Mis amigos Steemians-Lectores, en la figura 1(b) les muestro un disco de superficie 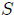 y de radio
y de radio 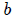 que se encuentra a una distancia
que se encuentra a una distancia 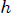 de un punto
de un punto 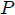 ubicado fuera de su eje de simetría, a una distancia
ubicado fuera de su eje de simetría, a una distancia 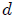 del mismo y en un plano paralelo al disco. Calcularemos el Angulo Sólido
del mismo y en un plano paralelo al disco. Calcularemos el Angulo Sólido 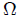 subtendido por el disco con respecto al punto
subtendido por el disco con respecto al punto 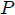 .
.
Observemos ahora la figura 4. Del triángulo 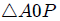 en la figura 4, usando el Teorema del Coseno, es posible determinar que,
en la figura 4, usando el Teorema del Coseno, es posible determinar que,
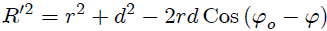
y usando el Teorema de Pitágoras en el triángulo 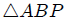 que,
que,
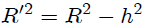
por lo tanto, al sustituir (13) en (14) y despejando 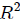 , obtenemos,
, obtenemos,
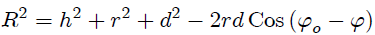
Además,
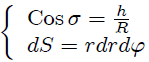
Ahora, al sustituir (14) y (15) en la definición 4, el Angulo Sólido buscado 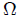 vendrá dado por,
vendrá dado por,
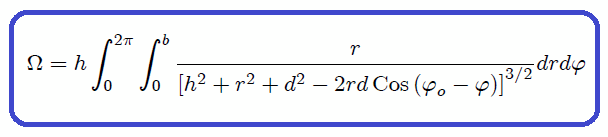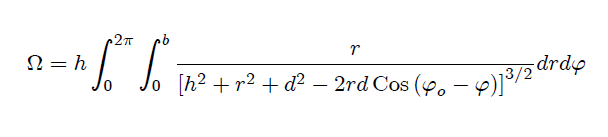
que es la integral que nos permite determinar el Angulo Sólido buscado. Si en la anterior expresión hacemos 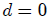 (
(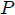 está en el eje de simetría) e integramos, obtendremos el resultado (6) como debería esperarse ya que, al hacer esto, el presente caso se reduce al estudiado en la sección anterior.
está en el eje de simetría) e integramos, obtendremos el resultado (6) como debería esperarse ya que, al hacer esto, el presente caso se reduce al estudiado en la sección anterior.
Mis estimados amigos Steemians-Lectores, la integración de la expresión (16) es bastante complicada, por no tener solución analítica en general. De hecho, se han hecho varios intentos por obtener soluciones usando métodos numéricos, métodos semianalíticos y aproximaciones, como pueden constatar en las referencias 9 hasta 16.
APORTES LOGRADOS, CON EL PRESENTE Y TODOS MIS ANTERIORES POSTS, ACERCA DEL ANGULO SOLIDO
Mis estimados y atentos Steemians-Lectores, con todo el trabajo por mi presentado hasta aquí acerca del Angulo Sólido, creo haber aportado en lo siguiente:
- Ampliar la bibliografía existente acerca del Angulo Sólido. En mi búsqueda, desde hace bastante tiempo atrás, no he encontrado textos dedicados exclusivamente a este tema de gran importancia en varias ramas de la ciencia y la tecnología.
- Lograr un contenido inteligible, con cantidad de claras ilustraciones y ejemplos.
- Proporcionar un texto de buena calidad sobre este tema para todas aquellas personas que inician sus estudios en Física Médica, donde los conocimientos sobre el ángulo sólido son de gran importancia, en especial, en aquellas áreas dedicadas a la dosimetría y detección de radiación. Lo mismo es válido para las otras áreas de la ciencia en que esta definición es útil.
PARA TERMINAR, SOLO FALTARIA UN POST DEDICADO A LAS APLICACIONES DE LA DEFINICION DE ANGULO SOLIDO, EL CUAL LES PRESENTARE MAS ADELANTE EN UN NUEVO POST. |
|---|

BIBLIOGRAFIA CONSULTADA Y RECOMENDADA
Aquí les presento, mis Steemians-Lectores, 17 textos que consulté para la elaboración del presente post.
Soldovieri C., T. & Viloria A., T. EL ANGULO SOLIDO Y ALGUNAS DE SUS APLICACIONES. Preprint, 2018. Página 77.
Mathar, R. J. SOLID ANGLE OF A RECTANGULAR PLATE. Max-Planck Institute of Astronomy, May 2015. Página 1 - 9.
Tipler, P. A. & Mosca, G. PHYSICS FOR SCIENTISTS AND ENGINEERS. W. H. Freeman and Company, 6th edition, 2008. Página 753.
Faget, J. & Mazzaschi, J. TEMAS PROGRAMADOS DE FISICA - GENERALIDADES, volume 1. Editorial Reverté, S.A., 1976. pp. 121 - 135. Página 123.
Kaufman, A. A. GEOPHYSICAL FIELD THEORY AND METHOD - GRAVITATIONAL, ELECTRIC AND MAGNETIC FIELDS, volume A. Academic Press, INC., 1992. Páginas 12 - 22.
Eyges, L. THE CLASSICAL ELECTROMAGNETIC FIELDS. Dover Publications, 1972. Páginas 12 - 22.
Alonso, M. & Finn, E. J. FISICA - MECANICA, volume 1. Fondo Educativo Interamericano, S.A., 1970. Página 22.
Khadjavi, A. CALCULATION OF SOLID ANGLE SUBTENDED BY RECTANGULAR APERTURES. Journal of the Optical Society of America, 58(10):1417 – 1418, 1968.
Rowlands, G. SOLID ANGLE CALCULATIONS. The International Journal of Applied Radiation and Isotopes, 10(2 - 3):pp. 86 – 93, 1961.
Masket, A. V. SOLID ANGLE SUBTENDED BY A CIRCULAR DISKSOLID ANGLE SUBTENDED BY A CIRCULAR DISK - LETTERS TO THE EDITOR. Review of Scientific Instruments, 30(10):pp. 950, October 1959.
Paxton, F. SOLID ANGLE CALCULATION FOR A CIRCULAR DISK. The Review of Scientific Instruments, 30(4):pp. 254 – 258, April 1959.
Naito, M. A METHOD OF CALCULATING THE SOLID ANGLE SUBTENDED BY A CIRCULAR APERTURE. Journal of the Physical Society of Japan, 12(10):pp. 1122 – 1129, October 1957.
Smith, J. H. & Storm, M. L. GENERALIZED OFF-AXIS DISTRIBUTIONS FROM DISK SOURCES OF RADIATION. Journal of Applied Physics, 25(4):pp. 519 – 527, April 1954.
Jaffy, H. SOLID ANGLE SUBTENDED BY A CIRCULAR APERTURE AT POINT AND SPREAD SOURCES: FORMULAS AND SOME TABLES. Review of Scientific Instruments, 25(4):pp. 349 – 354, 1954.
Garrett, M. W. SOLID ANGLE SUBTENDED BY A CIRCULAR APERTURE. Review of Scientific Instruments, 25(12):pp. 1208 – 1211, December 1954.
Berne, E. THE CALCULATION OF THE GEOMETRICAL EFFICIENCY OF ENDWINDOW GEIGER-MÜLLER TUBES. Review of Scientific Instruments, 22(7):pp. 509 – 512, July 1951.


Estimados amigos Steemians-Lectores. Espero que la anterior información les sea de mucha utilidad. Como ya es costumbre, si tienen preguntas no duden en hacérmelas llegar pues, con mucho gusto, les atenderé. Igualmente, si tienen detalles que puedan nutrir o mejorar la anterior información, por favor, háganmelas saber. Hasta mi próximo post ¡Saludos a todos! 😁.
Si deseas leer más artículos científicos de buena calidad, no pierda el tiempo, visite las etiquetas #steemstem y #stem-espanol. Es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Unete al canal de @steemstem. También puedes visitar el blog @steemstem y obtener más información.


¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias por el apoyo @entropia.
¡Saludos!
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for the support @steemstem!. Regards.
Congratulations @tsoldovieri! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard:
Thanks!,
EXCELENTE !!!!
SALUTATIONS DU VENEZUELA
Gracias por tu apoyo amigo @soy-venezuelien. Saludos.
Hola @tsoldovieri como ya es costumbre impecable aporte!! Saludos fraternos y éxitos!!
Gracias por tu comentario y apoyo amiga @reinaseq.
¡Saludos fraternos para ti también!
Saludos estimado @tsoldovieri. Excelente trabajo y didáctica con la que nos presentas tu serie de angulo solido.Un material de primera. Mis felicitaciones
Muchas gracias mi amigo y colega @lorenzor. Material para beneficio de la comunidad. Saludos.
Fantástico desarrollo de las ecuaciones estimado @tsoldovieri
Estimado @carloserp-2000, muchas gracias por tu positivo comentario y apoyo. Saludos.
Congratulations @tsoldovieri! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Thanks!.
Gracias por montar este trabajo @tsoldovieri, voy a tomar en cuenta para un trabajo que estoy desarrollando, utilizando tus ideas. Gracias
Gracias por tu comentario y apoyo amigo y colega @germanmontero. Me alegra que pueda servirte de algo mi trabajo. Saludos.