ESTUDIO DEL FUNCIONAMIENTO DE LA TRANSFORMADA DE FOURIER (TF) A TRAVÉS DEL ANÁLISIS DE SEÑALES MUESTREADAS EN TIEMPO DISCRETO
Saludos nuevamente mis estimados lectores…!
Dentro del mundo de las comunicaciones, cuando hablamos de “transmisión de información” concretamente en un sistema de Telecomunicaciones, los procesos por los cuales atraviesan las señales de extremo a extremo se traducen en un sinfín de aristas sumamente complejo. Los estudios y análisis inherentes a las señales de una transmisión pueden ser abordados mediante la interpretación de sus componentes temporales y frecuenciales, es decir, el análisis en el dominio del tiempo y en el dominio de la frecuencia nos denotan el comportamiento eléctrico de las señales propiamente dichas.
En una entrega anterior (no tan reciente) explicaba que toda señal puede ser representada (y por tanto reconstruida) por la suma infinita de senos y cosenos, en esa oportunidad se definió La serie de Fourier como una forma sumamente practica de recuperar la onda trasmitida originalmente. Resulta que esta aplicación es válida cuando las señales son del tipo periódica, pero, ¿qué pasa cuando esto no es así?. Si nuestro estudio se extiende más allá de las señales periódicas, es necesaria la implementación de un nuevo concepto el cual deriva en principio de las series de Fourier. Para cubrir estos espacios se ha de abordar La Transformada de Fourier (TF) la cual es empleada para recuperar señales en el dominio del tiempo las cuales serán trasvasadas al dominio de la frecuencia, esto con la finalidad de interpretar las componentes armónicas que conforman el espectro en cuestión para su posterior reconstruccion en la etapa del circuito receptor.
Figura 0 ; Distribuida bajo licencia CC0 -- Fuente (Edición Propia)
Para el desarrollo de este texto se establecerá como punto de partida una suma de señales senoidales y cosenoidales , esto para enfocar al lector en la temática que comprende la Transformada de Fourier, seguidamente se presenta una de las expresiones que se tiene para formular la TF así como su aplicación en un ejemplo para el caso de una señal discreta ya muestreada, finalmente se encarara a través de la teoría de los espacios de Hilbert la demostración matemática que justifica a la TF.
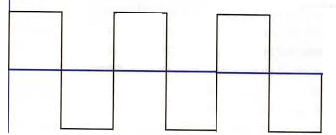
Figura N°1 Onda Cuadrada – Elaboración Propia
Para dar inicio, consideremos una señal del tipo cuadrada (Ver Figura Nº1), este es uno de los ejemplos clásicos que describen de forma óptima la sumatoria senoidal y cosenoidal; a simple vista se pudiera pensar que la forma de onda presentada es una sola señal, sin embargo, en los circuitos electrónicos la circulación de una onda cuadrada a través de sus componentes es el resultado del flujo de ondas simples (numerosas en cantidad) las cuales poseen distintas frecuencias pero que están definidas dentro de un espectro en común.
En palabras simples, la onda de la Figura Nº1 puede ser representada por la suma de ondas muchos más básicos, por ejemplo si sumamos las funciones 2sen(x)+sen(3x) se obtendrá:
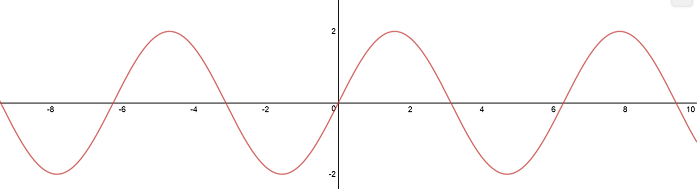
Figura N°2 Gráfica de la función 2sen(x) – Elaboración propia utilizando la herramienta en línea “DESMOS”
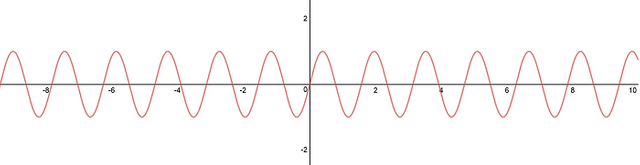
Figura N°3 Gráfica de la función sen(3x) – Elaboración propia utilizando la herramienta en línea “DESMOS”
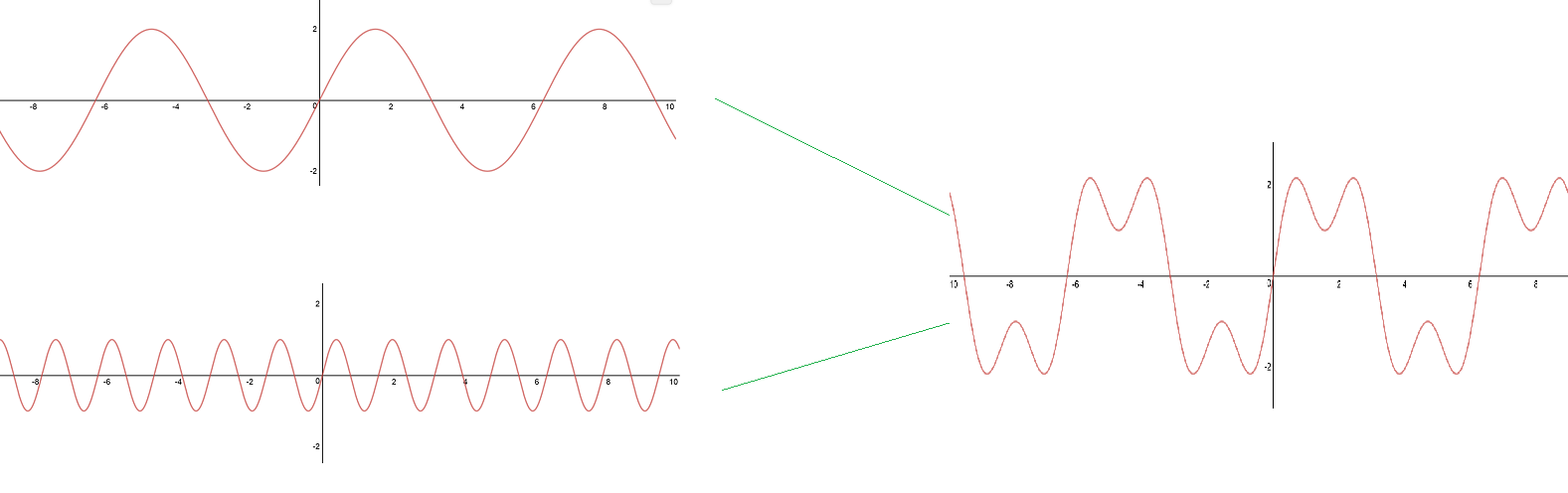
Figura N°4 Suma de las ondas 2sen(x) + sen(3x) – Elaboración propia
Si añadimos otra onda como 0,5sen(10x) la forma resultante se aproxima un poco más a la onda cuadrada:
Figura N°5 Gráfica de la función 0,5sen(10x) – Elaboración propia utilizando la herramienta en línea “DESMOS”
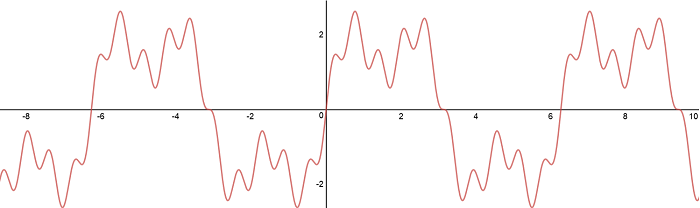
Figura N°6 Gráfica de la función 2sen(x)+sen(3x)+ 0,5sen(10x) – Elaboración propia utilizando la herramienta en línea “DESMOS”
Como se decía, esta es una suma infinita de señales senos y señales cosenos, entre más señales básicas se anexen se tendrá una mejor interpretación de la onda generada en la etapa de tx, no obstante, dicho razonamiento solo es válido en concepciones teóricas, pues en la práctica los sistemas operan con señales eléctricas finitas (lógicamente), por tanto se han de considerar solo un conjunto finito de frecuencias, acentuando como más importantes aquellas señales simples que comprendan amplitudes próximas a la señal original mejor conocidos como “armónicos”.
En efecto, la TF es una herramienta que discriminara más o menos de forma efectiva cada una de las señales simples, realizando comparaciones con respecto a la señal compleja (en este ejemplo, la señal compleja seria la onda cuadrada).
Sin más preámbulos, se presenta la expresión que rige la TF, esta es una ecuación referenciada en el proceso de muestreo de una señal (teorema de Nyquist) y que para efectos de esta explicación nos identifica uno que otro concepto clave complementario al estudio. Más adelante se indicara otra forma de expresar la TF pero en función del cálculo integral.
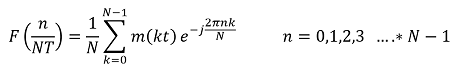
Donde N representa un bloque de datos contenedor de un número de muestras tomados de la señal, T es el periodo que se demora cada muestra en ser analizada o dicho de otra forma es el valor inverso a la frecuencia de muestreo f; “n” se define como un índice que indica el número de la frecuencia que se quiere obtener (frecuencia 0, frecuencia 1, frecuencia 2 …) y m(kT) es la muestra tomada en el instante de tiempo kT.
Aplicando valores enteros de n a la expresión dada, se obtiene que:
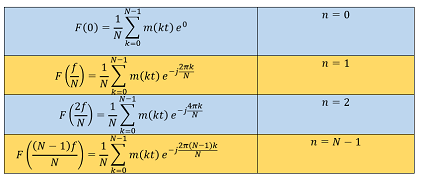
Tabla N°1 Desarrollo de la TF aplicando valores enteros de n — Elaboración Propia
Nótese que se ha rescrito el periodo T en términos de la frecuencia de muestreo (T=1/f).
Para el primer caso n=0 se obtiene una frecuencia nula 0Hz, que no es más que la componente continua de la señal.
En cuanto al desarrollo de cada uno de los sumatorios se aprecia que los valores en el intervalo medio de las muestras (entre 0 y N/2) se relacionan o mejor dicho, son exactamente iguales para el intervalo N/2 y N-1, esto significa que bastara con solo hacer los cálculos para una de estas dos mitades. Si se quiere ver más allá este concepto, hay que recordar el teorema de muestreo de Nyquist, el cual indica que la mitad de la frecuencia f de muestreo se corresponde con el ancho de banda de la señal, de allí el razonamiento anterior.
Entre mayor sea el número de muestras N mejor será la interpretación de la señal en el dominio de la frecuencia, pero como se decía, el intervalo de frecuencias en un sistema electrónico corresponde a un número finito de estas; si el proceso de muestreo es más sofisticado esto incidirá con la complejidad del circuito requerido.
A continuación, estudiaremos un ejemplo dando valores a las variables que se definieron. En este estudio se parte de la referencia de una señal genérica que bien puede representar cualquier tipo de señal definida en el espectro a abordar.
Dada una señal, consideramos que es muestreada a 20000 muestras por segundo tomando en cuenta un bloque de 100 datos. En definitiva la duración total de este muestreo será de 0.01 segundos.
Desarrollando la transformada de Fourier:
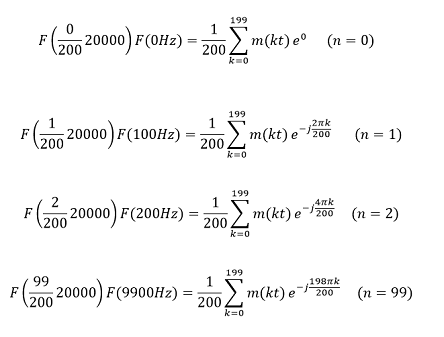
Como se puede notar la resolución en espectro entre cada una de las señales es igual a 100 Hz.
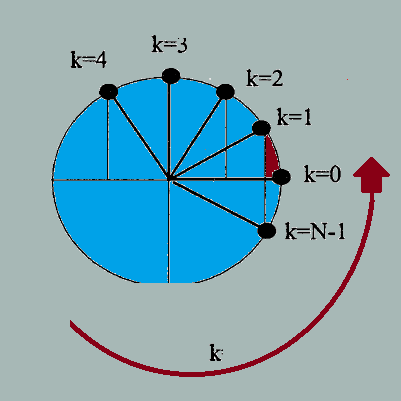
Figura Nº7 Rotación del número complejo en función de k -- Elaboración Propia
La expresión de la TF queda en función de los valores que tome “k”, más específicamente determinara el valor del argumento de la exponencial, esto se traduce (si se observa con detenimiento a la exponencial) que la velocidad angular será igual a 2πn y saltara conforme k/N (discretamente) , es decir la rotación de este número complejo será algo como lo que describe la Figura Nº7.
Estos “saltos” que realiza el número complejo pueden ser rescritos en función de senos y cosenos:
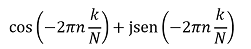
Muy importante…
Cada vez que el bloque de las muestras se compare (multiplicación de la muestra por senos y cosenos) con la función exponencial y éste a su vez sea muy parecido al seno o coseno por el que se multiplica cada muestra, se obtendrá un valor sumamente alto, ya que al operar cada valor positivo del seno y coseno por los valores positivos de la señal (igual para los valores negativos) se tendrá una suma de todos los elementos. Si por el contrario la señal no coincide con los senos y cosenos al sumar todos los productos, los valores positivos y negativos se anularan.
En palabras simples, al comparar una señal con ondas sinusoidales más básicas de distintas frecuencias y estas a su vez formen parte de la composición original, el resultado del sumatorio de la TF es distinto de 0 (porque esta es una frecuencia importante), en el caso que estas frecuencias no tengan nada que ver con la señal de partida, el resultado tiende a 0.
En el siguiente ejemplo se ilustra el funcionamiento de la TF tomando como referencia un estudio de muestreo realizado por Bobadilla (2000) a la señal descrita por 4sen(2x)+2sen(6x) cuya frecuencia de muestreo fue de 20HZ.
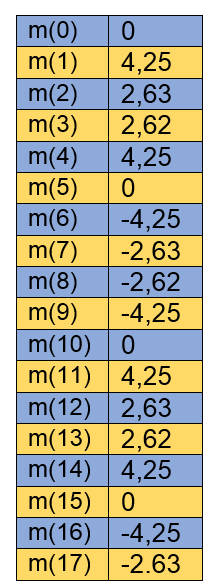
Tabla Nº2 Recopilación de los valores muestreados para la señal 4sen(2x)+2sen(6x) – Elaboración propia, datos de Bobadilla (2000)
Se desarrolla entonces los valores de n para determinar las frecuencias de estudio:
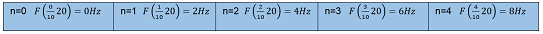
La TF desarrollada para la frecuencia de 2 Hz (cuando n vale 1 e iniciando en la muestra 7) nos queda:
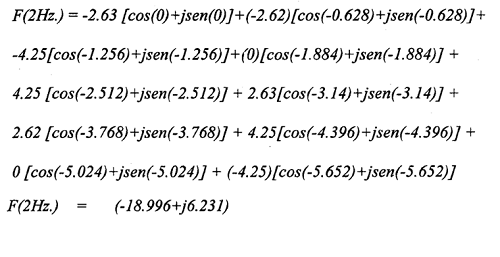
Este número complejo es rescrito en función de su módulo para expresar el nivel de energía contenido en la frecuencia estudiada:
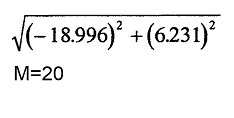
Este es un resultado que indica la importancia de esta componente frecuencial; para un n=2 , es decir, para la frecuencia de 4Hz se obtiene:
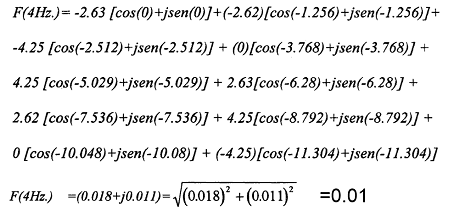
Este módulo es bastante bajo, por lo que su importancia dentro del espectro es despreciable y por tanto la frecuencia no es tomada en cuenta.
Con este ejemplo se ha podido deslumbrar el funcionamiento de la expresión de la TF, como se aprecia es un proceso relativamente sencillo (pero algo extenso), el desarrollo de esta transformada continua para los siguientes valores enteros de n, sin embargo es suficiente con los dos casos postulados (n=1 y n=2) para captar la idea. Si se continúa el desarrollo, se tendrán valores próximos a 0 y valores más altos (como se explicaba previamente), el circuito electrónico encargado de realizar esta operación discriminara cada uno de estos módulos descartando los valores nulos.
Estos cálculos son procesados por un ordenador (circuito) y generalmente es aplicada una variación que ayuda a simplificar dichos cómputos, esta variación es la FFT o transformada rápida de Fourier, la cual es capaz de reconstruir el espectro frecuencial con suficientes valores de n.Acá les dejo un video explicativo donde se ve con claridad lo estudiado en este texto:
Fundamentación Matemática de la TF
A continuación se procede a detallar desde un enfoque matemático la formalización de la Transformada de Fourier; para esta demostración serán empleadas nociones del espacio de Hilbert el cual es un espacio infinito dimensional que guarda mucha relación con los espacios euclidianos tradicionales, de hecho, varias de las operaciones entre los vectores que se describirán coinciden con las operaciones convencionales, como el producto escalar, ortogonalidad, producto entre vectores, etc.
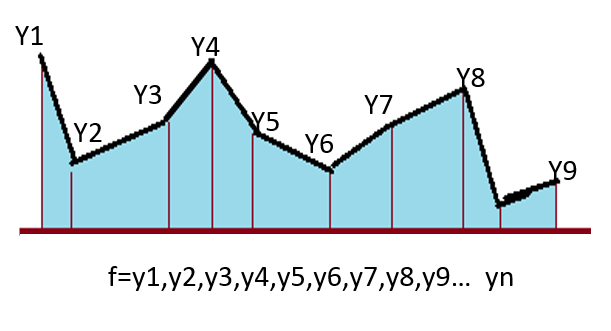
Figura Nº8 Grafica de una función discreta – Elaboración Propia
Comenzamos por decir que las características que se les atribuyen a los espacios n-dimensionales serán aplicadas a funciones discretas. Esta acción se justifica ya que las distintas muestras que se toman de este tipo de funciones son consideradas como las componentes de un vector de múltiples dimensiones. (Ver Figura nº8).
Para el caso de un espacio de Hilbert el valor de n tiende a infinito y la distancia entre componentes se ve reducida a 0, por tanto las funciones de estudio en estos espacios serán del tipo “continuas”.
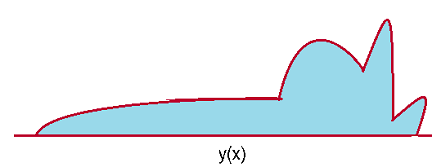
Figura N°9 Función en un espacio de Hilbert – Elaboración Propia
Entendido lo anterior, se define la suma de vectores como la adición entre funciones y el producto escalar vectorial como la multiplicación de un número por una función cualquiera. Estos serán los cimientos de toda la deducción que se desarrollara.
Pues bien, para calcular la longitud de un vector en espacio euclidiano se sabe que:
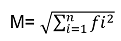
Es decir, el módulo M de un vector es igual a la raíz cuadrada de la suma de sus componentes al cuadrado. Para el caso que nos interesa, en espacios de Hilbert se tiene que la longitud de la función f viene dada por:
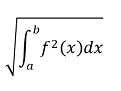
Para el producto escalar entre dos vectores f y g se tiene que:
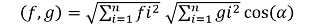
Su equivalente en el espacio de Hilbert :
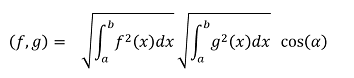
Y finalmente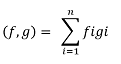 
Se corresponde con: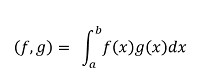 
Ya estamos casi listos…
Hasta el momento solo se ha definido la forma que se tiene para operar estas funciones.
Hablemos de la ortogonalidad:
Dentro del dominio de un espacio de Hilbert dos o más funciones serán ortogonales si el producto escalar de estas da como resultado 0 (como en cualquier espacio finito). Para un sistema de coordenadas (que es donde estará concentrada toda la acción) se tendrán “n” funciones ortogonales entre sí que representaran cada uno de los planos; lo que nos interesa saber es que función describe la proyección de todos estos ejes. Para un plano en dos dimensiones se sabe que:
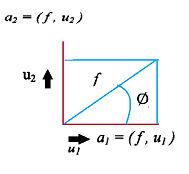
Figura N°10 Pproyección de un vector con respecto a sus componentes – Elaboración Propia
En pocas palabras lo que expresa la figura 10 es que dado un numero cualquiera de vectores “ui” perpendiculares entre si y de longitud 1, la obtención del vector resultante estará determinada mediante la proyección de cada uno de estos vectores respecto a cada plano. Llevando esta noción a la nomenclatura de Hilbert se tiene entonces:
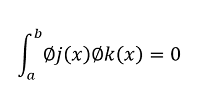
De forma análoga se define la ortonormalidad como:
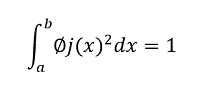
Asumiendo la progresión geométrica de una exponencial compleja (la cual define la forma de onda de una señal):
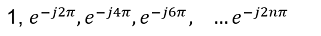
Se define la función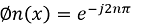 
Recordando que esto se puede rescribir como:
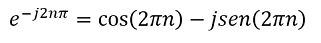
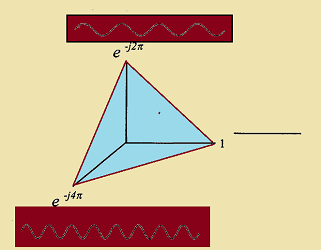
Figura N°11 Proyección de la progresión exponencial en 3 dimensiones – Elaboración Propia
Una función f(x) estará dada por:
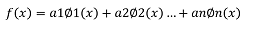
De todas estas ecuaciones, es importante decir que lo que más “interesa” es saber cuál es la proyección que tiene "an" en los demás planos, es decir, si sabemos ”que es an” habremos conseguido las componentes vectoriales que definen las frecuencias de una señal, en otras palabras, se tendrá el equivalente en el dominio dela frecuencia de una señal. Entonces se tiene que:
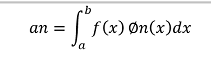
Donde ∅n(x) se había definido en función de la exponencial compleja, rescribiendo:
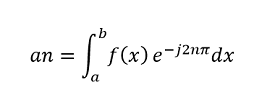
Y esta es la expresión que define la transformada de Fourier para una señal en tiempo continuo.
Cualitativamente hablando, al realizar el producto escalar entre la señal que se quiere analizar y la exponencial compleja, para cada valor que tome n (0,1,2 …) se obtendrá una frecuencia en específico, para cada situación está frecuencia será una porción del total que se compone de la onda original; si existe alta ortogonalidad entre la señal y un valor de la exponencial por consecuencia del índice n entonces la frecuencia resultante no será tan importante (despreciable) al momento de reconstruir el espectro de la frecuencia.
Para el caso de señales discretas, donde ya la señal ha sido muestreada se tiene entonces:
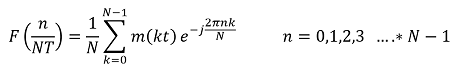
Con esto damos por finalizado el estudio que da sustento teórico a la TF. Son muchas las aplicaciones que tiene esta transformada en las telecomunicaciones, para un ejemplo más práctico , puede remitirse a mi publicación: TÉCNICAS EN COMUNICACIONES DIGITALES – MULTIPLEXACIÓN POR DIVISIÓN DE FRECUENCIAS ORTOGONALES (OFDM) en donde se realiza el cálculo de un TF para señales “pulso” donde el resultado de esta operación nos denota la pauta para ubicar componentes frecuenciales entre distintas ondas y así establecer la modulación OFDM.
REFERENCIAS
-STALLINGS, WILLIAM ; COMUNICACIONES Y REDES DE COMPUTADORES Séptima edición ; PEARSON EDUCACIÓN, S. A., Madrid, 2004.
-Antonio Artés Rodríguez Benavente; Comunicaciones Digitales; 2007.
-Johnsonbaugh; Matemáticas discretas; México 2005
