The Physics Behind Musical Sound from Different Kind of Musical Instruments
Hello, I Hope you all are fine and I welcome you to my blog once again and thanks for the constant encouragement.
If you missed what I Learnt last week click here to see some pretty amazing stuffs I discovered last week like Hippopotomonstrosesquipedaliophobia lol I know you want to know what kind of phobia is that.
Introduction
Musical sounds are in waves, a longitudinal wave. Which means the travelling of the wave oscillates, that is it moves back and forth, in the same direction that the wave is moving . A string, brass or wind instrument use a special kind of wave which is standing waves.
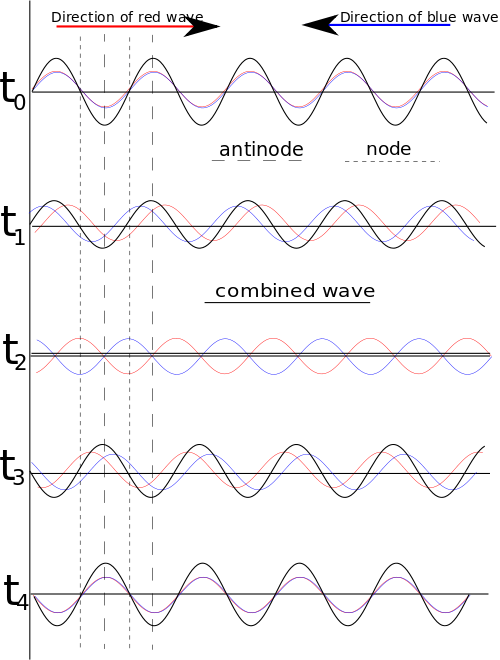
a standing wave oscillates in time but whose peak amplitude profile does not move in space.¦source
Standing wave is a wave that looks like it is not moving, it's amplitude may change but it is not travelling anywhere. Standing wave is the result of two other things waves do which are reflection and interference.
Reflection: Reflection is what happens when a wave reaches the end of a path and then moves back along thesame path. That is an example of what happen when you send a pulse down a fixed rope, it reaches the end and then it comes back. Reading from Wikipedia, let's see what reflection is
When you send a continuous wave down the rope, that is where interference comes into play. The waves reaches the end of the road and then it is reflected but there are peaks on the way, as the peaks pass each other, they interfere with one another and also changing their sizes.Reflection is the change in direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated.¦source
Taking about other frequencies, the reflected waves interface in such a way that you end up with the way that seams to stay perfectly still with only it amplitude changing and that is typical example of a standing wave which happen in the strings, air and pipes. That is what makes the pleasant sound we call music.
Standing waves with different frequencies correspond with different musical notes. Understanding how standing waves operate, first we need to understand the anatomy.
The points along the standing wave whereby the wave is having minimum amplitude is called the node while the points that have the maximum amplitude are called the antinodes which are formed in open boundaries and particles. An example of a node is the end of a vibrating guitar string.
Musicians makes their music using the frequency of this standing waves. The nature of this waves depends on what the end of the strings look like. Knowing how waves travelling down a rope get reflected differently depending on weather the end of the rope is fixed or loosed just like when they tune the guitar some strings are tight and some are not very tight, like I wrote up the wave depends on what the end of the rope looks like which is synonymous to the music produced depend on the end of the string.
The answer depends on whether the medium is fixed in space or free to move at its end. For example, if the pulse is moving through a rope and the end of the rope is held firmly by a person, then it could be said that the pulse is approaching a fixed end. On the other hand, if the end of the rope is lying on the floor such that it is free to move up or down when the pulse reaches its end, then it could be said that the pulse is approaching a free end.¦source
The properties of a standing wave would be different depending on weather it is made with a string with 2 ends fixed or pipe with 2 ends open in a case of a wind instrument or a situation where by a string had one end fixed and the other not fixed or a pipe where one end is open and the other is not.
A spring with to fixed end like in the piano is he simplest way to understand standing waves because we know that no matter what, the wave made by a fixed string would have at least 2 nodes with one at each end and in its most basic format, there would be just one antibodies in the middle. This basic kind of standing wave is know as the Fundamental.
Fundamental is the simplest standing possible wave that exist with the fewer nodes and antinodes. There are other more complex standing waves we can have which are Overtone.
Overtone builds up the fundamental by incriminating each overtime at the node and antinode, each of the overtone is related to the fundamental wave and all the overtones are related to each other. Together the fundamental wave and the overtone makes up what is known as Harmonic.
The fundamental is the first harmonic and the overtones are higher numbered harmonics. In each node and antinode, pad is added to the standing wave. The number of the harmonic goes up then we be having 2nd harmonic, 3rd harmonic and so on.
Physics expresses harmonics in terms of wave length sometimes, taking for example a spring with 2 fixed ends, the fundamental come exactly half of the the wave length. The second simplest standing wave you can have a string of 2fixed ends with 3 nodes with 1 at each ends and 1 in the middle plus 2 antinode between the nodes, it is called the second harmonic the string holds exactly 1wave length and also the 3rd harmonic, it has 4 nodes and 3 antinodes and the strings hold 1.5 wave length. You might have noticed a pattern from my explanation, for a standing wave, only a given length of spring. The number of the wave length that fit on the string is equal to the number of harmonic divided by 2. Now when you understand the wave length, you can figure out the aspect of wave that musicians care about most which is the Frequency.
Now we know that wave length multiply by frequency is the velocity which would be thesame for each harmonic so standing wave will be equal to velocity divided by wavelength. For the fundamental of two fixed ends, the wave letter is 2times the strings length so the frequency of the fundamental standing wave known as the fundamental frequency is equal to the velocity divided by 2times the length.
For standard wave frequency
For two fixed ends
Fundamental Frequency of 1st Harmonic
Lets see the frequency with the second harmonic.
Here, there are 3 nodes and 2 antinodes. The frequency would be equal to velocity divided by 2times the length of string which is twice the fundamental frequency as shown below
Then for 3rd harmonic
from the pattern we are seeing we can just used the formula below
The formula above is one of the ways of defining harmonic which is the number of the harmonic is equal to the number you multiply by the fundamental frequency to get the harmonic frequency.
This maths is what makes the musical instrument works. When you press down a key on the piano, it makes a standing wave in that string. Every string in a piano is tuned to its fundamental frequency that depends on its length, mass and tension corresponding to a given note.
For standing wave with 2 fixed ends, we can relate wave length, frequency, velocity, number of the harmonic and length of the string. We can do the same thing for standing wave with 2 loose end taking for example an open pipe (a flute), standing waves in a pipe of 2 open ends is kind of the opposite of the wave with two fixed ends it has a node in the middle and 2 antinodes at the edges. The fundamental standing wave for a pipe with 2 open ends would have 2 antinodes, second harmonic would have 3 antinodes and 2 nodes and so on but wat harmonic still cover the same number of wave length. The difference in both is that they starts with a node for the fixed and and for the fixed end it starts with an antinodes. The equations for wave length and frequency for standing wave with 2 one ends would be the same as they were as standing waves for 2 fixed ends.
Conclusion
All of this explains is why musical instrument sounds differently even when they are playing the same note. When you play a note you are creating a fundamental wave plus some of the other harmonic, the overtones and for each instrument different harmonics would have different amplitudes and therefore sound louder. Considering the physics of standing waves, instruments that have pipes with one closed end would create the even numbers harmonic that is why key A on the saxophone different from the key A on the keyboard those that play instruments can relate.
References
https://en.m.wikipedia.org/wiki/Wave_interference
https://en.m.wikipedia.org/wiki/Reflection_(physics)
https://en.m.wikipedia.org/wiki/Standing_wave
http://www.physicsclassroom.com/mmedia/waves/free.cfm
If you write STEM (Science, Technology, Engineering, and Mathematics) related posts, consider joining #steemSTEM on steemit chat or discord here. If you are from Nigeria, you may want to include the #stemng tag in your post. You can visit this blog by @stemng for more details.

Thanks for your time
@osariemen








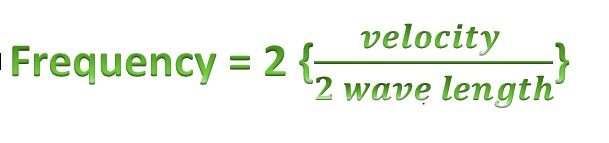
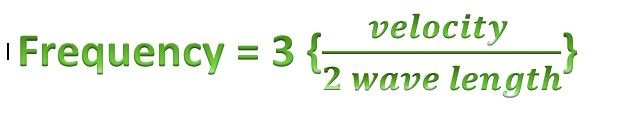
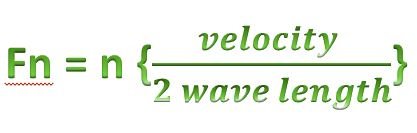

@Osariemen, thank you for using the naijapidgin tag.
We encourage and support minnows.
Join us on discord: https://discord.gg/5SR8CH4 for more fun and to submit your posts for curation.
You like what we are doing and would like to support us? Join our trail here: https://steemauto.com/dash.php?i=15&id=1&user=naijapidgin