[Ted Theory Vol. 2 : Factor Analysis]

Ted Theory Vol. 2를 기술하기전에 전제 조건이 필요하여 WanTED 공지를 제시하였다.

Ted Theory에서 가장 중요한 Factor에 대한 서술부터 진행할 예정이다. Ted Theory를 다시한번 살펴보면

T_B 항이 논하고자 하는 내용이다. 이를 Ted Method를 통해 예를 들어서 보여주었다. 이에 대해 좀더 자세하게 살펴보기전에 우리는 물리 용어에 대한 이해를 먼저 하고 지나가야겠다.

물리를 배우면 우리는 벡터와 스칼라에 대한 용어를 먼저 접하게된다. 우리가 이해하고 넘어갈 내용은 벡터에 대한 내용이다. 벡터는 크기와 방향을 가진 양에 대한 정의이다.

P(BF)=I×A(I: 정보량, A: 정보이동 가속도)

Ted Method에서 이를 예시를 통해서 설명하였다. 그렇다면 여기서 질문을 해본다. 어느 Factor가 벡터일까?

물론 사람들의 A에 대해 벡터라고 정의하는데 있어서는 이견이 없을 것이다. 하지만 I가 즉 m이 벡터라고 생각해보지는 않았는가 우리가 존재하는 Reference Point는 상수로 보이지만 이또한 움직이는 존재이다. 이를 그림을 통해서 살펴보도록 하자.

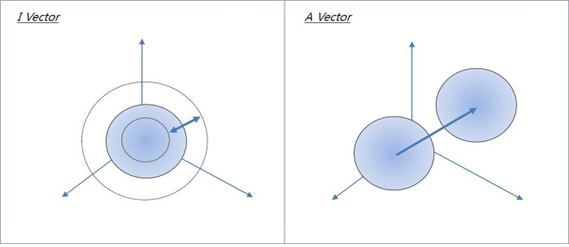
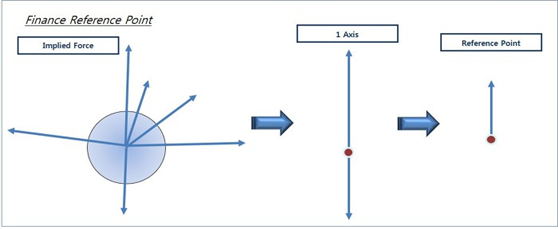
그림에서 보는바와 같이 I는 커지는 방향과 작아지는 방향이 있다. 그리고 벡터라고 인지하고 있는 가속도의 방향이 있을 수 있다. 이러한 벡터는 주식과 같이 위와 아래의 방향만 가지는 경우 3차원의 벡터를 1차원으로 선형으로 볼 수 있고 이러한 선형은 우리가 보이는 Reference Point에 의해 결과값이 보이게 되는 것이다.

이번에는 대유위니아의 매수와 매도에 따라 이러한 부분 및 실제 예측하는 부분에 대한 내용을 서술해보겠다.

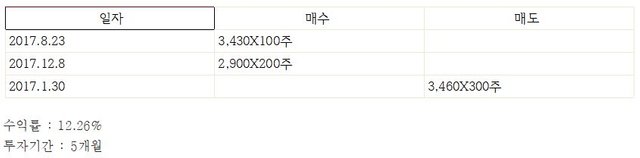
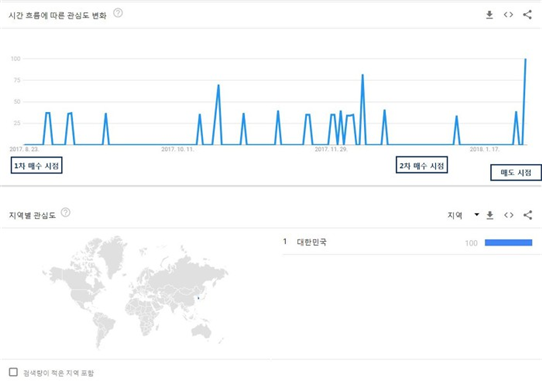
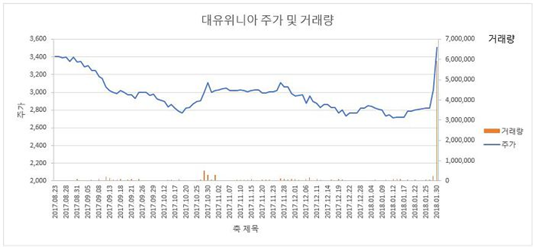
M&A를 통해 정보 및 정보의 가속도에 의한 검토를 진행하였다.
기업선별에 있어서 기업에 대한 분석을 통해 T_B 예측을 통한 거래를 진행하였다. M&A의 경우에는 벡터적인 요소가 가미되어있어 이러한 테스트를 진행하기에 적절한 케이스였다.
대유위니아는 사업의 다각화가 필수적인 기업으로 정보량이 적은 시점을 시작하였다. M&A 발표가 임박한 시점에서 거량이 폭발하는 것을 알 수 있고 우리가 보는 방향성을 알 수 있었다.

친구에게 이러한 얘기를 한적 있다. 공을 던지면 아래로 떨어진다. 하지만 던지는 시점에서 땅이 올라가면 더이상 떨어지는 곳이 높아진다고 했다. 즉 이러한 벡터에 의해 보이는 것은 내재적 가치에 의해 지지가 될 수 있다.

출처: http://tedvc.com/?page=1 [Value Creator TED]