Function generation in Octave from scratch part 3

What Will I Learn?

Greetings, in this tutorial we will continue focusing on making, editting functions in Octave by transforming our mathematical problems into computer based friendly algorithims.

• You will learn the usage and importance of 'for' cases,
• You will learn Octave's panels and it's properties,
• You will learn function writing in Octave,
• You will learn transfering your problems into functions,
• You will learn execution and debugging of a function via command window.

Requirements

• Octave 4.2
• Basic knowledge on coding
• Basic knowledge on sequences

Difficulty

• Basic

Tutorial Contents

To summarize, the third part of function generation in Octave tutorial will be mostly related with using for statement to solve and simply our problems. In order to that we must first remeber what we have done in previous parts and then manage a way to implement for case to the problems we solved in previous part.


Initially a for statement is needed or used when an action must be repeated in a desired order. Like counting, loops or simultaneous processes. Unlike if case a for case can be runned multiple times till the end point is reached. Each for case has a beginning, end and a condition part.


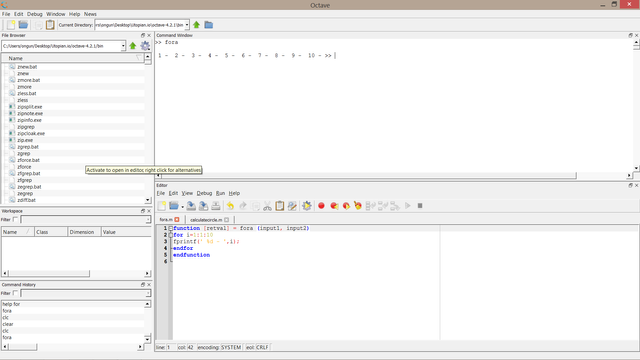
To begin with, it is useful to do a counting example with for. In this exercise our goal is to gather an output of numbers having the counting property from 1 to 100 with an increase rate of one. In other words, the output must be all the integers from one to hundred. To full fill that purpose below code was written in Octave's function panel,

function [retval] = fora (input1, input2)
for i=1:1:10
fprintf(' %d - ',i);
endfor
endfunction

The above code will generate numbers from 1 to 10 by giving a space and then a dash symbol like 1 - 2 - 3 ... Running the code gives us our desired answer as follows,

To extend our knowledge and try to solve another common problem, this time our task it to write a function which is capable of calculating factorial of any function. To begin with as usual we must first define the function, define that we will use function,

function [retval] = fora (input1, input2)

This code is capable of generating the function. Next the user input implemented,

number1 =input('Which factorial you want to calculate: ');

Next to calculate factorial the input number must be bigger than zero. Moreover for zero the factorial or result must be equal to one according to its definiton. Thereby first an if statement is used able to check whether the entered number is greater or equal to zero.

if(number1>=0)

When its greater or equal than one we can declare our another variable f which will be multiplied with its plus one and summed later to display the overall result,

f =1;

The reason to equal f to one is basicly because of factorials definition. Each calculation should start from one upto the user entered number, which we called it as number1 in our function. Later we need a for statement to multiply each number from one to the number1. To do that below code was written,

for i=1:1:number1
f = f * i;
endfor

Then to conclude we will call a print, display function that is capable of showing the overall result,

fprintf(' %d ',f);

But for other cases when number1 is not great or equal to zero we must prompt a warning message like "Entered number cannot be smaller than one!" to do that below code was written,

fprintf('Entered number cannot be smaller than one!');

And implemented in the overall code. As a result the overall code became,

function [retval] = fora (input1, input2)
number1 =input('Which factorial you want to calculate: ');
if(number1>=0)
f =1;
for i=1:1:number1
f = f * i;
endfor
fprintf(' %d ',f);
else
fprintf('Entered number cannot be smaller than one!');
endif
endfunction

Once we run the code below results were obtained,

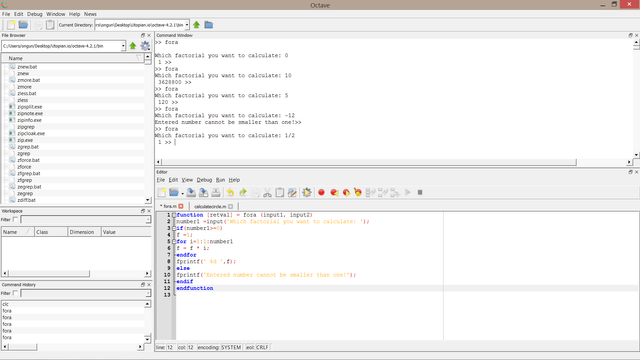
This is quite close to the solution of the problem. But there are few wrong points like factorial calculation for non integers which we will debug in our following tutorials. Moreover we will begin the transformation of complex mathematical expressions into functions like finite series and sigma, pi notation.

Curriculum

• Function generation in Octave from scratch part 1
• Function generation in Octave from scratch part 2
• Advanced drawing with Octave
• Two and three dimensional plotting with 'Octave'
• Solve and plot your equations with Octave!

---

Posted on Utopian.io - Rewarding Open Source Contributors

---