MATHEMATICAL EXPLANATION - TRANSFORMED FROM FOURIER
Hello friends !
Welcome to a new installment of my publications on the science of mathematics this time I will be talking about the TRANSFORMED FOURIER, a very complex mathematical procedure that is applied a lot in my area of engineering, to determine the behavior of electromagnetic waves as well as is also used for the application of other engineering procedures, below is a mathematical explanation of the fourier transform, I invite you to observe this interesting post.
Fourier Transform
The Fourier transform, named after Joseph Fourier, is a mathematical transformation used to transform signals between the time (or spatial) domain and the frequency domain, which has many applications in physics and engineering. It is reversible, being able to transform in any of the domains to the other. The term itself refers to both the transformation operation and the function it produces.
In the case of a periodic function in time (for example, a continuous musical sound but not necessarily sinusoidal), the Fourier transform can be simplified for the calculation of a discrete set of complex amplitudes, called coefficients of the Fourier series. They represent the frequency spectrum of the original time-domain signal.
The Fourier transform is an application that matches a function f with another function g defined in the following way:
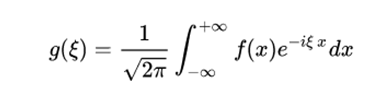
Where f is L ^ 1, that is, f must be an integrable function in the sense of the Lebesgue integral. The factor, which accompanies the integral in definition, facilitates the enunciation of some of the theorems referring to the Fourier transform. Although this way of normalizing the Fourier transform is the most commonly adopted, it is not universal. In practice, the variables x and E are usually associated with dimensions such as time -second- and frequency -herz- respectively, if the alternative formula is used:
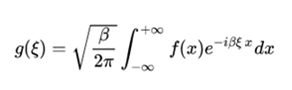
the constant B cancels the dimensions associated to the variables obtaining a dimensionless exponent.
The Fourier transform thus defined has a series of continuity properties that guarantee that it can be extended to larger function spaces and even spaces of generalized functions.
Its applications are many, in areas of science and engineering such as physics, number theory, combinatorics, signal processing (electronics), probability theory, statistics, optics, wave propagation and other areas. In signal processing, the Fourier transform is usually considered as the decomposition of a signal into components of different frequencies, that is, g corresponds to the frequency spectrum of the signal f.
The branch of mathematics that studies the Fourier transform and its generalizations is called harmonic analysis.
Definition
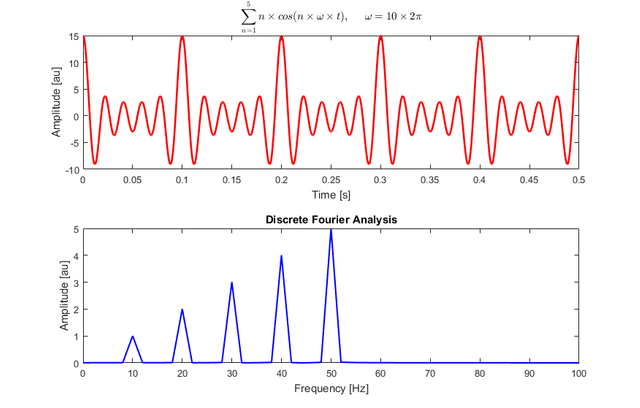
The Fourier transform is basically the frequency spectrum of a function. A good example of this is what the human ear does, since it receives an auditory wave and transforms it into a decomposition in different frequencies (which is what is finally heard). The human ear perceives different frequencies as time passes, however, the Fourier transform contains all the frequencies of the time during which the signal existed; that is, in the Fourier transform a single frequency spectrum is obtained for the entire function.
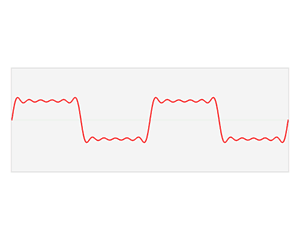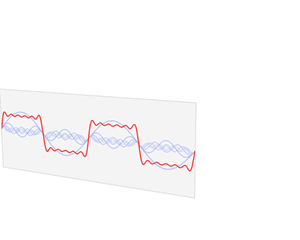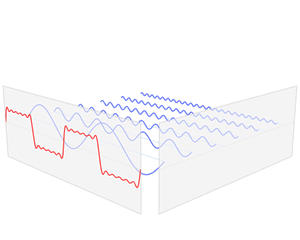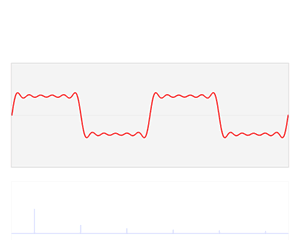
The Fourier transform relates a function in the time domain, shown in red, with a function in the frequency domain, shown in blue. The component frequencies, extended for the entire frequency spectrum, are represented as peaks in the frequency domain.
Formal definition
Let f be an integrable Lebesgue function:
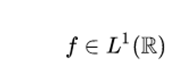
The Fourier transform of f is the function
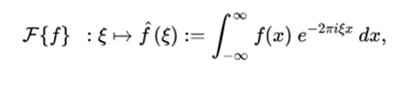
This integral makes sense, because the integrand is an integrable function. A simple estimate shows that the Fourier transform F (f) is a bounded function. Also by means of the dominated convergence theorem it can be shown that F (f) is continuous.
The inverse Fourier transform of an integrable function f is defined by:
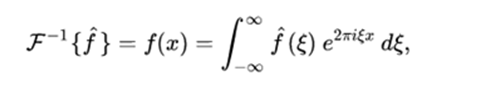
Note that the only difference between the Fourier transform and the inverse Fourier transform is the negative sign in the exponent of the integrand. The Fourier inversion theorem formulated below justifies the name of the inverse Fourier transform given to this transform. The negative sign in the exponent of the integrated indicates the transposition of juxtaposed complements. These complements can be analyzed through the application of variance for each function.
Investment Theorem
The basic idea of the inversion theorem is that given a function f, the inverse Fourier transform applied to the Fourier transform of f results in the same original function, in symbols:
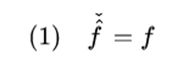
However, the result formulated in this way is not always valid, because the domain of the Fourier transform as we have defined it in the first paragraph of this article is not invariant, that is, the Fourier transform of an integrable function is not necessarily integrable.
To formulate the investment theorem we need to find spaces of functions that are invariant under the Fourier transform. In fact, there are numerous possibilities, the most natural from the technical point of view being Schwartz's space of rapidly decreasing functions. However, here we take a more direct path to formulate a statement:
Theorem. The space of complex functions f defined on the line such that f and the Fourier transform of f are integrable, is invariant by both the Fourier transform and the inverse Fourier transform. Also for a function f in this space, the investment theorem (1) is valid.
Another possibility to formulate an investment theorem is based on the fact that the Fourier transform has many natural extensions.
Basic properties :
The Fourier transform is a linear application:
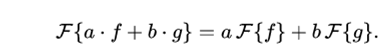
The following properties are valid for an absolutely integrable function f:
- Change of scale:
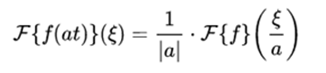
- Translation:
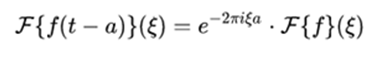
- Translation in the transformed variable:
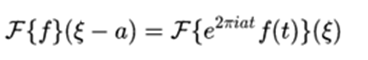
- Transform of the derivative: If f and its derivative are integrable,
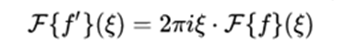
- Derived from the transform: If f and t → f (t) are integrable, the Fourier transform F (f) is differentiable
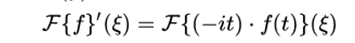
These identities are demonstrated by a change of variables or integration by parts.
In what follows, we define the convolution of two functions f and g on the line as follows:
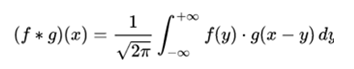
Again the presence of the factor in front of the integral simplifies the statement of the results as follows: If f and g are absolutely integrable functions, the convolution is also integrable, and it is equal:
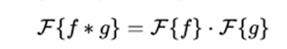
An analogous theorem for convolution in the transformed variable can also be stated,
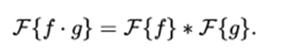
but this requires some care with the definition domain of the Fourier transform.
References
- https://homepages.inf.ed.ac.uk/rbf/HIPR2/fourier.htm
- http://www.thefouriertransform.com/
- https://en.wikipedia.org/wiki/Fourier_transform
- Bailey, David H .; Swarztrauber, Paul N. (1994), "A fast method for the numerical evaluation of continuous Fourier and - Laplace transforms" (PDF), SIAM Journal on Scientific Computing, 15 (5): 1105-1110, doi: 10.1137 / 0915067.
- Boashash, B., ed. (2003), Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Oxford: Elsevier Science.
- Bochner, S .; Chandrasekharan, K. (1949), Fourier Transforms, Princeton University Press.
- Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw-Hill.
- Campbell, George; Foster, Ronald (1948), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc ..
Hello,
Copying/Pasting full texts without adding anything original is frowned upon by the community.
These are some tips on how to share content and add value:
Repeated copy/paste posts could be considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.
If you are actually the original author, please do reply to let us know!
Thank You!
More Info: Abuse Guide - 2017.
This is really good. I am a student of Signals and systems myself and I have studied the Fourier transform. It is always good to convert a signal to its frequency to study it properly.
thank you friend for your comment, you are grateful for the support, it is important to share the knowledge.
Interesting read. Personally, I have used FFT to transform discrete time domain into frequency domain to study response.
@joseferrer : Fourier and Laplace transform are my dearest topics. Btw I don't know if you saw the recent video from 3blue1brown youtube channel about intuitively explaining Fourier transform. It is very beautiful and can be used as an addendum to this article. Let me post the link here. Resteeming the article. Keep up your original work :)
I really hate the math, but I am thankful for this mathematical function. Without Forunier Transform a lot of the work I do in the lab would not be possible. Thank you for this article! Cheers!
Spanish wiki page (https://es.wikipedia.org/wiki/Transformada_de_Fourier): La transformada de Fourier, denominada así por Joseph Fourier, es una transformación matemática empleada para transformar señales entre el dominio del tiempo (o espacial) y el dominio de la frecuencia, que tiene muchas aplicaciones en la física y la ingeniería. Es reversible, siendo capaz de transformarse en cualquiera de los dominios al otro. El propio término se refiere tanto a la operación de transformación como a la función que produce.
Google translate:
The Fourier transform, named after Joseph Fourier, is a mathematical transformation used to transform signals between the time (or spatial) domain and the frequency domain, which has many applications in physics and engineering. It is reversible, being able to transform in any of the domains to the other. The term itself refers to both the transformation operation and the function it produces.
This is identical to your text