EVALUACIÓN DEL ESPESOR DEL AISLANTE TÉRMICO REQUERIDO EN EL SISTEMA DE SECADO DE BANDEJA TIPO ESTRELLA CON FLUJO BIDIRECCIONAL (PARTE II)
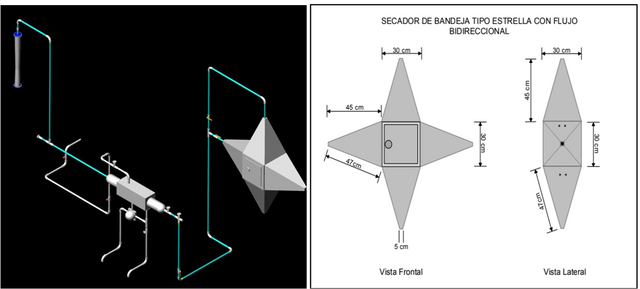
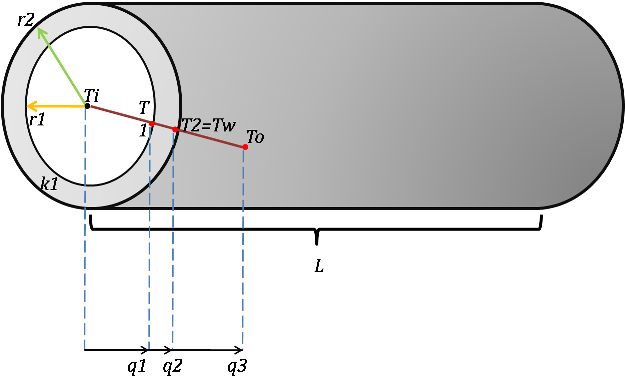
EVALUACIÓN DEL ESPESOR DEL AISLANTE TÉRMICO REQUERIDO EN EL SISTEMA DE SECADO DE BANDEJA TIPO ESTRELLA CON FLUJO BIDIRECCIONAL



CÁLCULOS

- Determinación de la temperatura de película (Tf).
Es el promedio aritmético de las temperaturas de la superficie y del flujo libre. De esta forma, se supone que las propiedades del fluido se mantienen constantes en esos valores a lo largo de todo el flujo. En el caso de convección natural "T∞" corresponde a la temperatura del fluido circundante.

- Determinación del coeficiente de expansión volumétrica.
Representa un parámetro que permite conocer el aumento del volumen del fluido tomando en cuenta el aumento de temperatura que sufre el mismo.

- Determinación del número de Rayleigh.
El número de Rayleigh es el producto de los números de Grashof y de Prandtl. Es un valor adimensional que se usa para estimar cuando en un fluido se inicia la convección. Este número depende de la densidad y la profundidad de un fluido, el coeficiente de expansión térmica, el campo gravitatorio, el gradiente de temperatura, la difusividad térmica y la viscosidad cinemática.

- Determinación del número de Nusselt.
El número de Nusselt medio para la convección natural hacia distintas configuraciones geométricas, se puede calcular a partir de la siguiente ecuación, En la cual los valores de las constantes (C y m) se pueden tomar de los datos referenciales para placas y cilindros verticales.

- Determinación del coeficiente de transferencia de calor.
Al despejar de la Ecuación para el número de Nusselt el coeficiente convectivo, se tiene:

- Determinación del área de transferencia de calor.
Representa el área superficial de contacto con el fluido. A continuación, se muestran las expresiones utilizadas para distintas configuraciones geométricas.

- Determinación de la velocidad de transferencia de calor.
La razón de la transferencia de calor por este mecanismo es proporcional a la diferencia de temperatura y se expresa de manera conveniente por la ley de Newton de enfriamiento.


RESULTADOS
De manera análoga se determinaron las pérdidas de calor para los demás tramos de tubería.
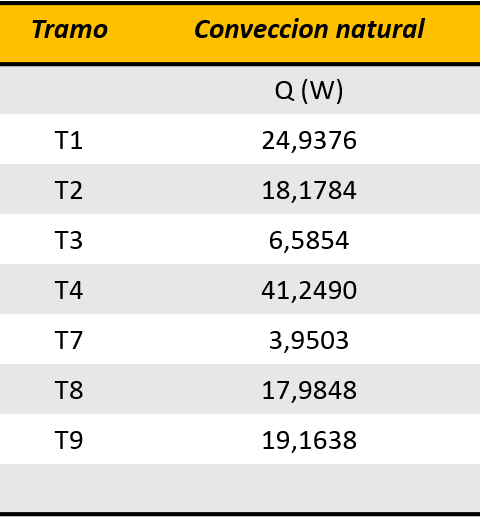
Comparando los resultados obtenidos para la perdida de calor por conveccion natural con los resultados obtenidos para la perdida de calor por conveccion forzada interna podemos notar la diferencia en la perdida de calor obtenida entre ambos mecanismos de transferencia de calor.
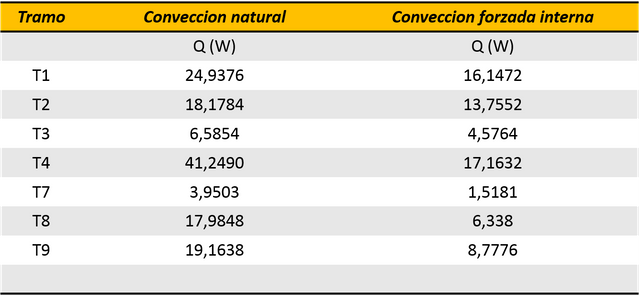
Sin embargo, al no cumplirse con lo establecido por la ley de la conservación de la energía, fue necesario repetir los cálculos a partir de un proceso iterativo en las temperaturas de pared y de salida, obteniéndose como resultados para ambos mecanismos.
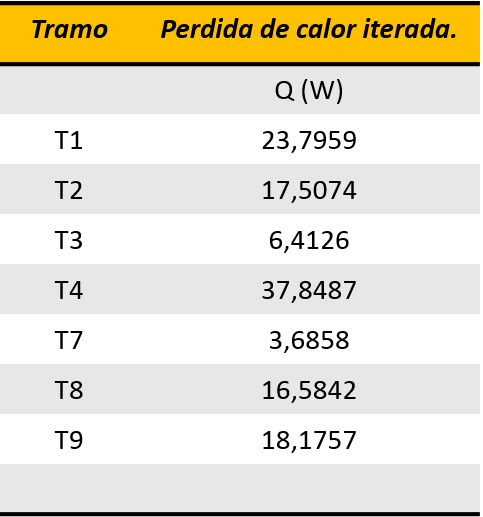

ANÁLISIS DE LOS RESULTADOS
Tomando en consideración lo establecido por la ley de la conservación de la energía, las determinaciones de las pérdidas de calor se llevaron a cabo en función de obtener tanto para convección forzada interna como para convección natural una misma pérdida de calor, para lo cual fue necesario un proceso iterativo en los valores de temperatura involucrados en el sistema en estudio.
Es importante señalar que la diferencia entre los valores determinados de pérdida de calor para cada tramo radica principalmente en las longitudes, puesto que a mayor longitud mayor será el tiempo de residencia del flujo y por consiguiente el tiempo de contacto entre el mismo y la pared de la tubería, generándose así mayores pérdidas de calor. Lo antes expuesto se puede apreciar en el tramo 4 vertical.
Es importante acotar que los tramos 5 (paralelo horizontal) ,6 (paralelo horizontal) y 10 (perpendicular vertical) no se tomaron en cuenta para el estudio de pérdida de calor, ya que, las longitudes de los mismos (0,028m, 0,051m y 0,053m respectivamente) fueron muy pequeñas, asimismo las temperaturas de entrada y salida de los tramos descritos fueron similares, lo que se traduce a un gradiente de temperatura alrededor de cero.

REFERENCIAS
·
- Cengel, Yunus A. (2007). Transferencia de calor y masa. Tercera Edición México, Editorial: McGraw-Hill.
- Perry, R. H. (1997). Manual del Ingeniero Químico. México: McGraw-Hill.
- Donald Q. Kern (1965). Procesos de transferencia de calor. Editorial: McGraw-Hill.
- Guía de prácticas de laboratorio de operaciones unitarias I. Universidad Politécnica Territorial del Oeste de Sucre “Clodosbaldo Russián”
- Geankoplis, Christie (1998). Procesos de transporte y operaciones unitarias. México, Editorial: Continental S.A

Nice read. I leave an upvote for this article thumbsup