Ecuaciones diferenciales aplicadas en la Física

Foto tomada y editada por @chetoblackmetal
Introducción.
La victoria de la ciencia moderna no fue completa hasta que estableció un principio más esencial, o sea, el intercambio de información libre y cooperador entre todos los científicos. A pesar de que esta necesidad nos parece ahora evidente, que las herramientas matemáticas han sido de estímulos en otras disciplinas, como soporte de su base de investigación, como es el caso de la ciencia de la Física, pone énfasis en aquellos aspectos que son de utilidad en la modelización y resolución de problemas que plantea dicha disciplina científica, hay que tener claro mis compañeros lectores amante del conocimiento, que no se puede comprender profundamente la Física sin abordar seriamente el estudio de su principal herramienta, la Matemática, con énfasis en la resolución de problemas de condiciones iniciales, debidos a que estudiar fenómenos físicos, en general, se encuentran leyes que no vinculan entre sí a las magnitudes que caracterizan el fenómeno, sino que involucran relaciones entre esas magnitudes y sus derivadas.
Definición básica.
Ecuación diferencial, es una ecuación que relaciona de manera no trivial a una función desconocida y una o más derivadas de esta función desconocida con respecto a una o más variables independientes, de tal forma que podemos decir también una ecuación en la cual la función incógnita aparece afectada por una o más derivadas. En otros niveles de compresión menciono, que las ecuaciones diferenciales tienen una solución analítica sencilla, la mayor parte de las veces es necesario realizar aproximaciones, estudiar el comportamiento del sistema bajo ciertas condiciones.
Desde mi concepto la investigación de muchos problemas de ciencia y tecnología puede reducirse a la solución de tales ecuaciones de esta temática .
Las ecuaciones diferenciales de primer orden y a los problemas de valor inicial, en esta parte se estudian los métodos clásicos de solución tales como variables separables, ecuaciones lineales, homogéneas, exactas, cuasi-exactas y por sustituciones de diferentes niveles de variable incógnitas o variables a estudiar según el caso. Por otro lado tenemos las ecuaciones diferenciales de orden superior y los diferentes métodos de solución ya sean por superposición, reducción de orden, las cuales las determinan por sus coeficientes indeterminados, anulador y variación de parámetros, de tal forma que nos permita problemas modelados.
El orden de una ecuación diferencial ordinaria.
Un modo de clasificar ecuaciones diferenciales ordinarias es según su orden. Diremos que una ecuación diferencial ordinaria es de orden n, o que es una ecuación de n-ésimo orden, si la derivada de mayor orden de la función desconocida en la ecuación es la derivada enésima.
dy/dx + 2xy e^(-x²)= 0
(ω´) ² +2t ³ ω´-4t ² ω= 0
dy/dx + 2xy e^(-x²)= 0
(ω´) ² +2t ³ ω´-4t ² ω= 0
dx/dy= 3t²+4t+2/2(x-1)
Cita textual. Ecuaciones diferenciales: una introducción moderna Escrito por Henry Ricardo, pág.: 3.
Partiendo desde esta cita podemos entenderlo a atreves de del siguiente ejemplo:
dy/dx = 2x.
En donde describimos la ecuación de la siguiente manera, la variable independiente (v.i) es x, la variable dependiente (v.d) es y.
Bueno ahora mis queridos lectores hay que tomar en cuenta es la forma de resolverlo, porque que es lo que se quiere, es utilizar la ecuación de igualdad para dar repuesta a nuestra ecuación diferencial, por medio de la aplicación de derivada, dándonos una ecuación para ser sustituida en la ecuación diferencial.
Partiendo de la ecuación dy/dx = 2x.
Efectuamos lo siguiente.
ʃ dy = ʃ2xdx
Nos queda
y= 2x²/2 +c
Nos da la ecuación resultante
y= x²+c
Ya que tenemos nuestra ecuación, recuerdan que tenemos que remplazarla en la ecuación anterior realizando lo siguiente.
dy/dx = 2x.
d/dx(x²+c) = 2x
x= 2x es nuestra ecuación final como solución mis queridos compañeros.
Para X1=1
Y1=2(1)= 2
Para X2=2
Y2= 2(2)=4
Para X3=3
Y3= 2(3)=6
Tenemos la siguiente tabla:

Con la aplicación de Geogebra, graficamos nuestra ecuación resultante:
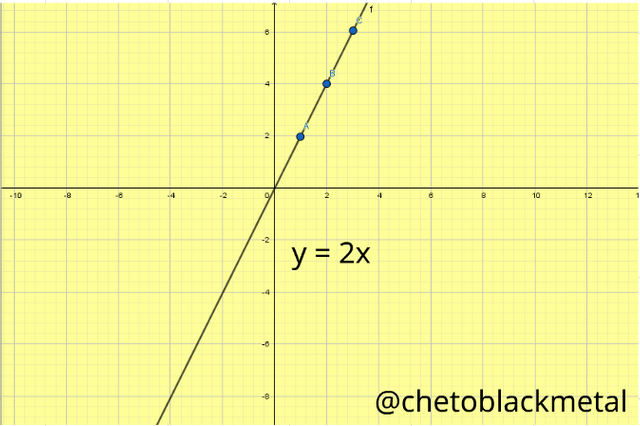
Gracias a las gráficas nos permiten ver y tener mejor una idea en la forma, que se manifieste visualmente la relación matemática en la ecuación que estamos trabajando mis compañeros lectores, esto importante al momento que se imparte una clase de esta índole y el abordaje matemático sobre el manejo de estas herramientas.(Gráfica elaborada por @chetoblackmetal)
Ya con lo anterior mencionado y explicado de los fundamentos básicos entremos en materia aplicado en la física. Ya este nivel lo plateare más técnico porque al estudiar fenómenos físicos, en general, se encuentran leyes que no vinculan entre sí, a las magnitudes que caracterizan el fenómeno donde se trabaja con magnitudes y otras forma de mediciones que se trabaja para la obtención de ecuaciones, que contienen no sólo la función incógnita de tal forma en forma escalar o vectorial de forma que nos encontraremos una o más derivadas de la misma dentro su planteamiento de investigación en su campo de estudio.
Comencemos a definir la ecuación bajo el concepto de la ley de desintegración radiactiva, en donde definimos dN, como el número de núcleo atómico, el intervalo de tiempo recodemos que los fenómenos físicos se trabajan en función de la magnitudes y el tiempo, la definimos con dt, es proporcional al número de núcleo presentes con N(t) con una constante k.
Tenemos como la siguiente ecuación.
dN(t)/dt= -Kn(t).
Lo importante de la ecuaciones diferenciales en el campo de la física es definir bien cada miembro de ecuación igualada.
Tenemos el siguiente caso abordando la ley de Newton, sobre la fuerzas de masa en donde una partícula de masa de manera constante con m, considerando que se mueve en una dimensiones espacial o en el espacio, con la aplicación fuerza F en función del tiempo t, con la disposición de la incógnita x y se conoce la velocidad v= dx/dt de la partícula de la masa en movimiento.
Se conoce la ecuación de la ley
F= ma, donde a = d²x/dt²
Realicemos la ecuación diferencia y nos queda:
m (d²x/dt²)=F
m (d²x/dt²)=F(txdx/dt)
Recordemos que la educación diferencial, sustituimos la primera ecuación para realizar nuestra ecuación en la igualación y también mis compañeros lectores se considera que la función incógnita es la función de dos o más variables para origen a una ecuación diferencial en derivadas parciales.
Me interese en esta parte para aclarar lo siguiente, porque en el campo de la física en su estudio de sistemas trabaja con número finito de grados de libertad, el cual nos conduce a ecuaciones diferenciales ordinarias, mientras que el estudio de medios continuos conduce a ecuaciones diferenciales en derivadas parciales.
Por eso la aplicación de esta herramienta de la matemática por la determinación de la función incógnita es el problema fundamental que ataca la teoría de ecuaciones diferenciales.
Conclusión.
Luego de conocer los aportes básico sobre la ecuaciones diferenciales y su aplicación, en el ámbito de la ingeniería, investigaciones de física, astronomía, también en la biología en el manejo de población bacterianas y sus propagación, darle importancias a la evolución y compresión de nuevos métodos de aplicación o abordaje matemático en ciencias como la física, que trabajen estudios de fenómenos y otros tipos de eventualidades que ocurren en la naturaleza, también quiero dar estés post, como un aporte al conocimiento como profesor mas ya allá de un salón de clase, el conocimiento hay que compartirla para que nazca nuevas idea y percepción en este contenido ya explicado, en un próximo publicación se continuando esta temática en la física, como el abordaje de ecuaciones diferenciales lineales.
Consultas bibliográficas.
Métodos Analíticos Para Ecuaciones Diferenciales Ordinarias J. J. Jiménez Zamudio, J. López García - 2007.
Introducción a las ecuaciones diferenciales ordinarias Celso Martínez Carracedo - 1991.
Ecuaciones diferenciales por C. Henry Edwards, David E. Penney - 2001.
Ecuaciones diferenciales por Víctor Jiménez López - 2000.
Ecuaciones Diferenciales En Física, por Raul Dante Rossign Carlos Maria Naon, James Zimmerhoff - 2017.


El uso y aplicación de las ecuaciones diferenciales es de suma importancia en la ciencia y la ingeniería, buena tematica educativa tocada por @chetoblackmetal. En espera de un nuevo tema relacionado con la misma temática. Saludos
Saludos @carlos84 por tu apoyo y tu valioso comentarios, si esta temática es muy importante en la ciencia
@chetoblackmetal, I gave you a vote!
If you follow me, I will also follow you in return!
Thanks for the support
Saludos buen trabajo académico @chetoblackmetal
Saludos y gracias por tu comentario
Gracia @ramonycajal y al equipo de cervantes por valorar y apoyar mi contenido académico
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...
Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.
Gracias por el apoyo y por valorar mi contenido
Corrige la palabra "somo" de la imagen.
Gracias ya lo corregí