Método de Separación de Variables Aplicado a un Modelo de Caída Libre Retardada por la Resistencia del Aire (Enfoque Analítico Matemático y Numérico Computacional)
Saludos estimados seguidores de Steemit y comunidad de #stem-espanol en general, continuando con las aplicaciones de las matemáticas en la ciencia, el día de hoy abordaré uno de los modelos utilizados para describir el movimiento de caída libre retardado por la resistencia del aire, uno de mis artículos anteriores se enfocó en un problema similar referente a la caída de un paracaidista, sin embargo, el presente artículo aborda una situación diferente.
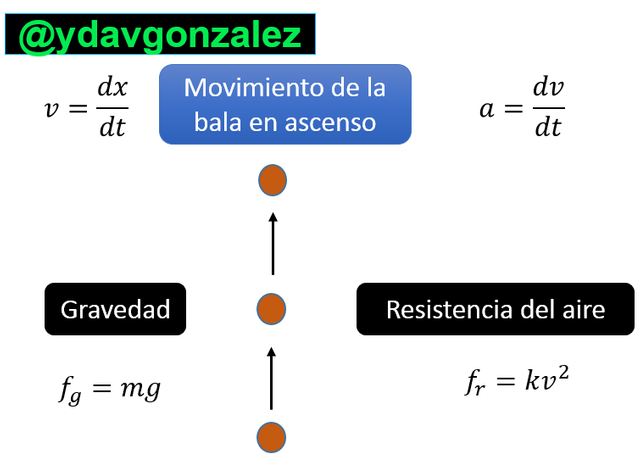
Movimiento de una bala en ascenso. Fuente: Elaboración propia.
Las matemáticas suelen ser utilizadas para estudiar diversos fenómenos del mundo real, por ejemplo, cuando se dispara cualquier tipo de proyectil, la leyes de la mecánica pueden utilizarse para describir este movimiento, muchas veces al aplicar dichas leyes aparecen ecuaciones diferenciales ordinarias que deben ser resueltas para obtener una solución que pueda interpretarse y ser interpretada en el mundo real.
De esta manera, las abstracciones matemáticas permiten modelar situaciones reales y describir su evolución en el tiempo, sin embargo, no basta solo con modelar los fenómenos, también se deben aplicar técnicas matemáticas para resolver los modelos obtenidos, en el caso del disparo de una bala hacia arriba el movimiento puede ser descrito teniendo en cuenta que se trata de un típico caso de caída libre retardada por la resistencia del aire, en este sentido, la física ha construido una serie de modelos para describir este movimiento, uno de los cuales se explica en el presente artículo.
El movimiento de una bala que es disparada hacia arriba puede ser modelado utilizando algunos postulados básicos de la mecánica teniendo en cuenta que se trata de un ejemplo de caída libre en el que interviene la resistencia del aire, diversas expresiones matemáticas pueden ser aplicadas para modelar este fenómeno.
Por ejemplo, la segunda ley de newton establece que la fuerza que actúa sobre la bala es siempre igual a
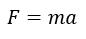
Donde (m) es la masa de la bala y (a) su aceleración, definiendo la dirección positiva hacia arriba se establece que una fuerza positiva actúa acelerando la bala hacia arriba y una fuerza negativa actúa generando un movimiento hacia abajo.
En el caso del movimiento de la bala existen dos fuerzas que componen la fuerza total que actúa sobre la bala, la primera es la fuerza de gravedad y la segunda la resistencia del aire, matemáticamente esto se expresa como:
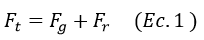
Donde Ft es la fuerza total, Fg la fuerza debida a la gravedad y Fr la resistencia del aire. La fuerza generada por la gravedad puede ser modelada teniendo en cuenta que dicha fuerza arrastra a la bala hacia abajo es decir en dirección negativa por lo tanto es igual a
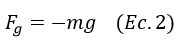
En el caso de la resistencia del aire se utilizan diversas expresiones para modelarla, en un artículo anterior se modelo utilizando la expresión
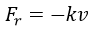
Donde v es la velocidad del objeto y k una constante de proporcionalidad, sin embargo, esta expresión no es la única utilizada para modelar la resistencia del aire, en el caso del disparo de proyectiles se suele utilizar otra fórmula para la resistencia del aire la cual se expresa como:
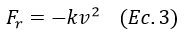
Se observa que la resistencia del aire es negativa debido a que actúa hacia abajo al detener a la bala en su ascenso, combinando las ecuaciones 1,2 y 3 se obtiene
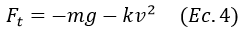
Teniendo en cuenta la segunda ley de newton
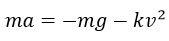
Recordando que la aceleración de un objeto en movimiento es equivalente a la razón de cambio de su velocidad en el tiempo (derivada), se puede sustituir la aceleración por:
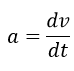
Obteniendo
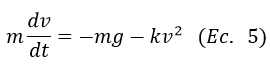
Ahora bien, esta expresión analiza el ascenso de la bala desde la perspectiva de la dinámica de las fuerzas involucradas, este análisis omite el cálculo de la distancia recorrida por la bala, si se quiere analizar la distancia se puede partir del hecho de que la velocidad de la bala equivale a la razón de cambio (derivada) de la distancia en el tiempo, es decir:
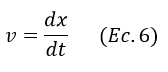
Según la regla de la cadena
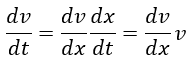
Luego (5) puede reescribirse como
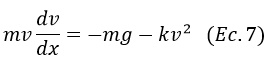
Esta Ecuación Diferencial Ordinaria involucra una derivada que incluye a la distancia, el método utilizado para resolverla se conoce como separación de variables y consiste en despejar en cada lado de la ecuación cada variable (v con dv) y (x con dx) y luego integrar ambo lados.
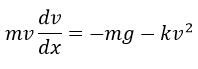
Dividiendo entre m
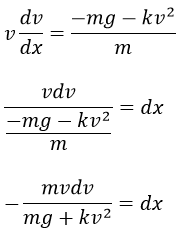
Integrando ambas expresiones se observa que
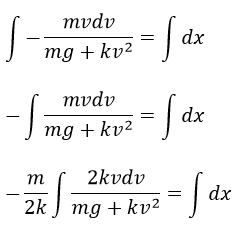
Realizando la sustitución
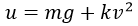
y
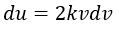
Se obtiene
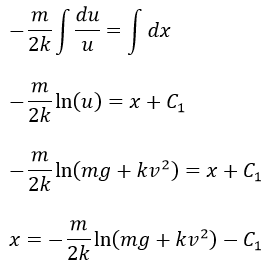
Cuando la bala es disparada se encuentra a cero metros de altura de su punto de partida, es decir, cuando v=v0 se cumple que x=0 por lo tanto
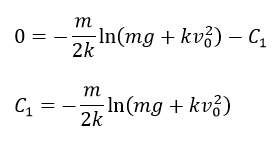
Al sustituir la constante de integración en la solución general se obtiene
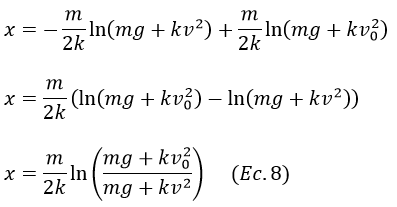
Ejemplo
Una bala es disparada hacia arriba con una velocidad inicial vertical de 988 m/s, si la bala posee una masa de 0,00356 kg y una constante de resistencia del aire de k=0,0000073 kg/m determine la altura máxima que alcanza la bala.
Para encontrar la altura x se necesita conocer la velocidad de la bala en ese instante de tiempo debido a la naturaleza del movimiento en ese instante la velocidad de la bala es de 0 m/s ya que en ese punto comenzará a caer, (se omiten las unidades para simplificar los cálculos).

Es decir, la bala alcanza una altura máxima de 1.298 metros antes de empezar su descenso, adicionalmente también se puede analizar la variación de la velocidad de la bala en el tiempo, para este fin se utilizará la ecuación número 5 obtenida con anterioridad
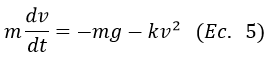
Dividiendo ambos lados de la expresión entre m
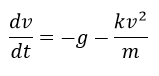
La solución de esta ecuación diferencial permitirá obtener el valor de la velocidad en cada instante de tiempo. En el problema planteado la masa de la bala es de 0,00356 kg y la constante de resistencia del aire de k=0,0000073 kg/m, por lo tanto, la ecuación diferencial se expresa como

Aplicando factor común y separación de variables
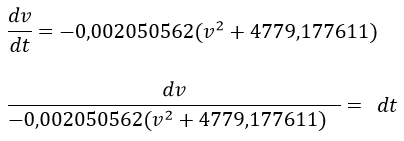
Integrando ambos miembros
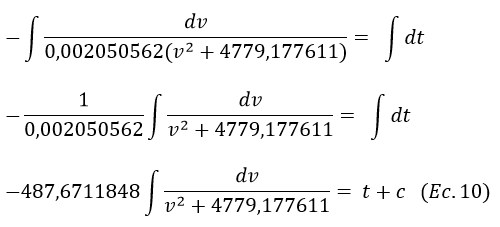
La integral del lado izquierdo puede ser resuelta utilizando la siguiente fórmula
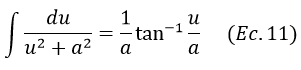
Para realizar la sustitución se debe observar que

Luego al sustituir la ecuación número 11 en la número 10 se obtiene
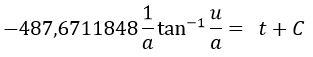
Reemplazando los valores de u y a
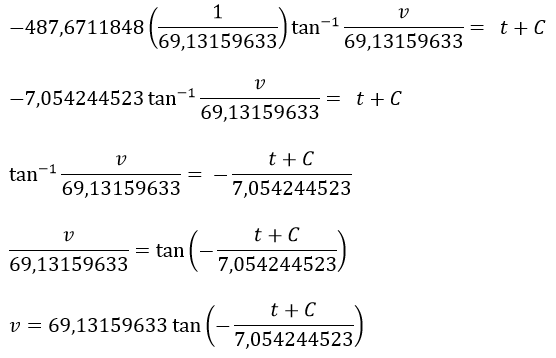
Debido a que según los datos del problema en el instante de tiempo 0 la velocidad inicial de la bala es de 988 m/s se cumple que

Al sustituir la constante de integración en la solución general de la ecuación diferencial ordinaria se obtiene
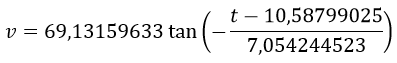

Fórmula para calcular la velocidad de la bala en función del tiempo de recorrido.
Esta función permite calcular la velocidad de la bala en cualquier instante de tiempo, si se desea determinar el tiempo que tarda la bala en ascender hasta el punto más elevado de su trayectoria se debe recordar que en dicho punto su velocidad es cero debido a que está a punto de empezar a caer , es decir:

Por lo tanto, la bala tarda 10,58799025 segundos en llegar hasta su punto más elevado que como se demostró se encuentra ubicado a 1298,234140 metros de altura.
Solución Numérica (Método de Runge-Kutta de 4° orden)
En el ejemplo mostrado en el presente artículo se pudo resolver la ecuación diferencial ordinaria aplicando métodos provenientes del análisis matemático, sin embargo, existen casos en que dichos métodos no son suficientes, ante esta realidad se han desarrollado una serie de métodos numéricos que permiten obtener aproximaciones bastante fiables a las soluciones analíticas de las ecuaciones diferenciales ordinarias.
Con el fin de garantizar la precisión en la solución se suele utilizar un método desarrollado en los años 1900 por los matemáticos Carl David Tolmé Runge y Martin Wilhelm Kutta el cual se conoce como el método de Runge-Kutta de 4° orden, este método es uno de los más utilizados en la actualidad debido a su alto grado de precisión y por ser programado de forma elemental, para obtener la solución numérica de la ecuación diferencial ordinaria mediante el método de Runge-Kutta de 4° orden solo se requiere una condición inicial.
Las formulas utilizada por este método son las siguientes:
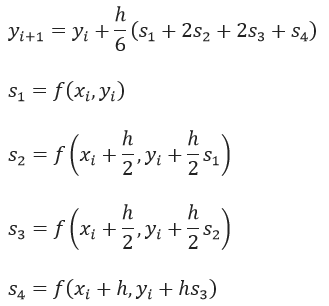
Donde h es el tamaño de paso, un valor bastante pequeño.
En líneas generales se inicia con la condición inicial y(x0)=y0, se estiman las cuatro pendientes s1, s2, s3 y s4 y mediante el promedio ponderado de estas pendientes se aproxima el siguiente valor de yi a partir del valor anterior.
Este método puede ser aplicado al problema mostrado en el presente artículo, recordando que la ecuación número 9 y la velocidad inicial de 988 metros por segundo permiten construir el problema de valor inicial:
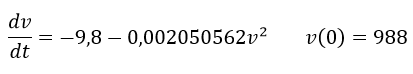
Debido a que la bala asciende hasta que t=10,58799025 segundos el intervalo llega hasta dicho punto es decir podemos aplicar el método de Runge-Kutta de 4° orden hasta un valor de t=10,5; si se selecciona un tamaño de paso de 0,25 se puede aplicar el método de forma eficiente.
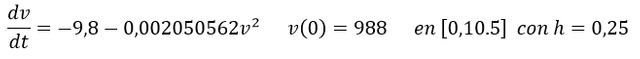
En el presente artículo se utilizó el Sistema de Algebra Computacional WxMaxima el cual permite aplicar este tipo de métodos numéricos, a continuación se muestra el Script utilizado
/*************************************/
/* MÉTODO DE RUNGE-KUTTA de 4° ORDEN /
/ Licdo Ysmael González /
/ U.C. Cálculo Numérico /
/ UNEFM 2016 /
/*************************************/
f(t,v):=-9.8-0.002050562v^2$ /Ecuación diferencial a resolver/
t0:0$ v0:988$ /Condición inicial t0 y v0/
tf:10.5$ delta:0.25$ /Valor final del intervalo tn y tamaño de paso/
fpprintprec:5$ /Número de cifras decimales/
sol(t):=69.13159633tan((10.58799025-t)/7.054244523)$ /Solución analítica de la EDO/
tn:t0$ n:0$ vn:v0$ iter:(tf-t0)/delta$
print("");
while n<=iter do
(
s1:f(tn,vn),
s2:f(tn+(delta/2),vn+(s1delta/2)),
s3:f(tn+(delta/2),vn+(s2delta/2)),
s4:f(tn+delta,vn+(s3delta)),
g:sol(tn),
ep:abs(g-vn)100/g,
print("It=",n," t=",float(tn)," V(t)=",float(vn)," V.E.=",float(g)," E.P.=",float(ep),"%"),
n:n+1,tn:tn+delta,vn:vn+(delta/6)(s1+2s2+2s3+s4)
);
Este programa genera la siguiente salida:
| Tiempo | v(t) | Sol. Aprox. | Error |
|---|---|---|---|
| 0.0 | 988.0 | 988.0 | 0.000% |
| 0.25 | 654.1 | 654.11 | 0.001654% |
| 0.5 | 487.98 | 487.96 | 0.003% |
| 0.75 | 388.35 | 388.33 | 0.003938% |
| 1.0 | 321.81 | 321.79 | 0.003897% |
| 1.25 | 274.12 | 274.11 | 0.003628% |
| 1.5 | 238.18 | 238.17 | 0.003332% |
| 1.75 | 210.07 | 210.06 | 0.003064% |
| 2.0 | 187.43 | 187.42 | 0.002833% |
| 2.25 | 168.75 | 168.75 | 0.002639% |
| 2.5 | 153.06 | 153.05 | 0.002477% |
| 2.75 | 139.64 | 139.64 | 0.002343% |
| 3.0 | 128.02 | 128.02 | 0.00223% |
| 3.25 | 117.84 | 117.83 | 0.002138% |
| 3.5 | 108.81 | 108.81 | 0.002062% |
| 3.75 | 100.74 | 100.74 | 0.002% |
| 4.0 | 93.458 | 93.456 | 0.001952% |
| 4.25 | 86.844 | 86.843 | 0.001915% |
| 4.5 | 80.795 | 80.793 | 0.001888% |
| 4.75 | 75.227 | 75.225 | 0.001872% |
| 5.0 | 70.072 | 70.071 | 0.001865% |
| 5.25 | 65.275 | 65.274 | 0.001867% |
| 5.5 | 60.789 | 60.788 | 0.001879% |
| 5.75 | 56.575 | 56.573 | 0.001901% |
| 6.0 | 52.597 | 52.596 | 0.001933% |
| 6.25 | 48.829 | 48.828 | 0.001976% |
| 6.5 | 45.245 | 45.244 | 0.002032% |
| 6.75 | 41.824 | 41.823 | 0.002102% |
| 7.0 | 38.546 | 38.545 | 0.002189% |
| 7.25 | 35.395 | 35.394 | 0.002295% |
| 7.5 | 32.357 | 32.356 | 0.002424% |
| 7.75 | 29.418 | 29.417 | 0.002583% |
| 8.0 | 26.566 | 26.565 | 0.002779% |
| 8.25 | 23.791 | 23.79 | 0.003025% |
| 8.5 | 21.082 | 21.082 | 0.003336% |
| 8.75 | 18.432 | 18.431 | 0.003739% |
| 9.0 | 15.831 | 15.831 | 0.004277% |
| 9.25 | 13.273 | 13.272 | 0.005026% |
| 9.5 | 10.748 | 10.748 | 0.006131% |
| 9.75 | 8.2518 | 8.2512 | 0.007909% |
| 10.0 | 5.7763 | 5.7757 | 0.01122% |
| 10.25 | 3.3155 | 3.3148 | 0.01946% |
| 10.5 | 0.863 | 0.8623 | 0.07464% |
Tabla N° 1 Variación de la velocidad en el tiempo según la solución Analítica y Numérica. Fuente. Elaboración propia.
En la tabla n° 1 se observa como disminuye la velocidad en el tiempo, se evidencia que tanto la solución analítica obtenida al resolver la ecuación diferencial ordinaria como la solución numérica al aplicar el método de Runge-Kutta de 4° orden arrojan valores muy cercanos. Recordando que la función de velocidad es la siguiente:
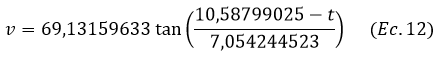
Se puede representar gráficamente como
Gráfica N° 1 Velocidad de la bala(m/s) en función del tiempo(s) durante el ascenso. Fuente: Elaboración propia mediante la herramienta https://www.desmos.com/
La altura de la bala se puede calcular teniendo en cuenta la ecuación número 8
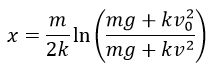
Al sustituir los datos del problema planteado

Al sustituir la ecuación 12 en la expresión anterior se obtiene

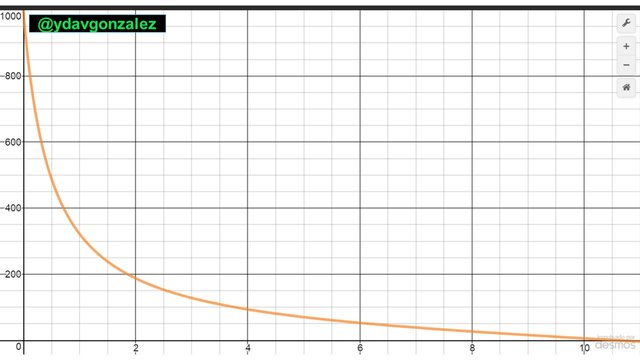
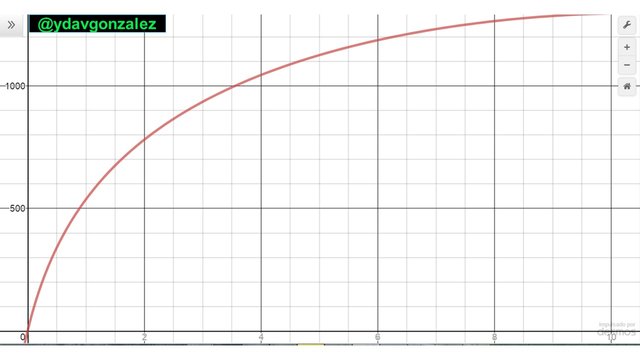
Gráficamente la altura en función del tiempo se observa en la siguiente imagen
Gráfica N° 2 Altura de la bala(m) en función del tiempo(s) durante el ascenso. Fuente: Elaboración propia mediante la herramienta https://www.desmos.com/
Conclusiones
- Existen diversos modelos que estudian la resistencia del aire, dependiendo del tipo de problema estudiado suele aplicarse cada uno de ellos.
- Las técnicas analíticas de resolución de Ecuaciones Diferenciales Ordinarias permiten obtener soluciones exactas pero no siempre pueden ser aplicadas.
- El Método de Runge-Kutta de 4° orden tiene una gran variedad de aplicaciones en la ciencia en general permitiendo obtener respuestas muy precisas a modelos matemáticos.
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editorial Limusa Willey.
González (2018) Modelado Matemático mediante Ecuaciones Diferenciales Ordinarias, Caso de Estudio: Caída Libre retardada por la Resistencia del Aire (Resolución mediante SCILAB) Disponible aquí.
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Saenz (2009), Cálculo Integral con Funciones Trascendentes Tempranas para Ciencias e Ingeniería. 2da edición Editorial Hipotenusa.
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.

Imagen de dominio público. Fuente: @steemstem
una gran referencia matemática
Gracias por el apoyo @karimuddinn
Felicitaciones! @ydavgonzalez. Gran talento en esta comunidad.
Gracias @elvigia por el apoyo, me alegra que revises mi perfil con frecuencia, Saludos.
Muy buen articulo. Me hubiera servido mucho en mis tiempos universitarios.
Así es, gracias por el apoyo @marcusantoniu26.
Excelente trabajo @ydavgonzalez, enalteciendo como siempre la aplicación de las matemáticas a problemas reales, contextualizado en este caso al problema de caída libre retardada por la resistencia del aire; en definitiva un problema de mucho de interés, muy bien abordado, con ese toque didáctico. Disfruté mucho de su lectura, saludos y muchos éxitos!!!
Gracias @eliaschess333 he visto que en tus artículos también usas mucha matemática, lo cual me agrada bastante, te agradezco que leas mis publicaciones.
Saludos.
Interesante método.
Felicitaciones por tu artículo, como siempre abordas los temas con gran cuidado y con bases sólidas que justifican tus procedimientos. Éxitos!
Gracias por tu comentario y por tomar algo de tu tiempo para leer y analizar mi trabajo, así es, en la ciencia las matemáticas permiten abordar diversos fenómenos físicos.
Saludos @isgledysduarte.
Espero seguir contando con tu apoyo en mis futuros artículos.
Excelente, la aplicación que le encuentras a la matemática en un problema de física, me gusto mucho tu artículo @ydavgonzalez.
Saludos @veronicacoli, que bueno que hayas leído mi post, gracias por apoyarme.
Espero seguir contando con tu apoyo en mis futuros artículos.
Te felicito @ydavgonzalez muy interesante la aplicación de este modelado matemático a través de un software. Un trabajo impecable y que nos muestra la importancia de las matemáticas para la descripción y abordaje de temas en las distintas ramas de la ciencia.
¡Felicitaciones!
Gracias por el apoyo, como químico también has tenido oportunidad de utilizar la matemática al estudiar diversos fenómenos de la ciencia.
Saludos @joseleogon.
Espero seguir contando con tu apoyo en mis futuros artículos.
Bonito problema de mecánica clásica, uno de los libros que posee esa teoría es el Marion (Dinámica Clásica). Buen trabajo @ydavgonzalez
Gracias por el apoyo, cuando tenga algo de tiempo lo revisaré.
Saludos @germanmontero.
Espero seguir contando con tu apoyo en mis futuros artículos.
Impecable como siempre!, es bastante practico mostrar el resultado numerico de este tipo de problemas.
Así es, los Sistemas de Álgebra Computacional permiten desarrollar estos métodos mediante el uso del ordenador y obtener una solución numérica muy aproximada a la solución real. De esta forma se combinan la matemática y la programación en pro de obtener resultados a problemas que describen fenómenos físicos.
Saludos @vjap55.
Espero seguir contando con tu apoyo en mis futuros artículos.